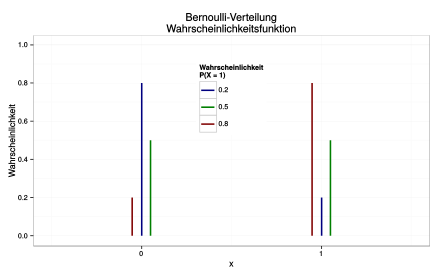
BERNOULLI分布の確率関数

(青)、

(緑)と

(腐敗)
1つのランダムサイズ ベルヌーリの分布 (Asも同様です ゼロワン分布 、 代替分布 [初め] また ブール分布 [2] 記述)は、可能なテスト出力が2つしかないランダムイベントを記述するために使用します。テスト出力の1つは通常です 成功 記述および補完的なテスト出力 失敗 。関連する確率
 成功のために、成功の確率が呼ばれ、
成功のために、成功の確率が呼ばれ、
 故障の確率。
故障の確率。
例:
指定 Bernouli-Attemp ( ベルヌーアン裁判 Jakob I Bernoulliによると)、この本は1937年に初めてでした 数学的確率の紹介 James Victor Uspenskyが使用します。 [3]
離散ランダムサイズ
 群衆の中に価値があります
群衆の中に価値があります
 それは ゼロワン分布 また。 ベルヌーリの分布 パラメーターで
それは ゼロワン分布 また。 ベルヌーリの分布 パラメーターで
![pin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c) 次の確率関数に従う場合
次の確率関数に従う場合
-
 。
。
分布関数は次のとおりです
-
 。
。
それからあなたは書きます
 また
また
 。
。
各個々の試みがベルヌーリ分布に十分である多くの独立した同一の試みは、ベルヌーリプロセスまたはベルヌーリシュテストスキームと呼ばれます。
期待値 [ 編集 | ソーステキストを編集します ]
パラメーターを使用したBernoulli分布
 期待値があります:
期待値があります:
-

これには、Bernoulliが分散したランダム変数について
 と
と
 と
と
 該当する:
該当する:
-

分散およびその他のストルマス [ 編集 | ソーステキストを編集します ]
Bernoulliの分布には分散があります
-

その理由は
 したがって
したがって
-
 。
。
したがって、標準偏差はです
-

および変動係数
-
 。
。
対称 [ 編集 | ソーステキストを編集します ]
パラメーター用
 ベルヌーイの分布は、ポイントの周りに対称的にあります
ベルヌーイの分布は、ポイントの周りに対称的にあります
 。
。
曲がった [ 編集 | ソーステキストを編集します ]
ベルヌーリの分布の曲がったものはです
-
 。
。
これは次のように表示できます。標準化されたランダム変数
 と
と
 Bernoulliは価値を分配しました
Bernoulliは価値を分配しました
 確率で
確率で
 オンと値
オンと値
 確率で
確率で
 。曲がった人のためにそれを手に入れます
。曲がった人のためにそれを手に入れます
-
![{displaystyle {begin{aligned}operatorname {v} (X)&=operatorname {E} left[left({frac {X-operatorname {E} (X)}{sqrt {operatorname {Var} (X)}}}right)^{3}right]\&=pcdot left({frac {q}{sqrt {pq}}}right)^{3}+qcdot left(-{frac {p}{sqrt {pq}}}right)^{3}\&={frac {1}{{sqrt {pq}}^{3}}}left(pq^{3}-qp^{3}right)\&={frac {pq}{{sqrt {pq}}^{3}}}(q-p)\&={frac {q-p}{sqrt {pq}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/444b272655aba54f608ed51507bd0de15adec89c)
金庫と過剰 [ 編集 | ソーステキストを編集します ]
ベルヌーイ分布の過剰はです
-

そして、それは曲率です
-
 。
。
瞬間 [ 編集 | ソーステキストを編集します ]
すべてのk-ten瞬間
 同じことで、適用されます
同じことで、適用されます
-
 。
。
その理由は
-
 。
。
エントロピ [ 編集 | ソーステキストを編集します ]
ベルヌーリ分布のエントロピーはです
-

ビットで測定。
モーダス [ 編集 | ソーステキストを編集します ]
ベルヌーリ分布のモードはです
-
 。
。
中央値 [ 編集 | ソーステキストを編集します ]
ベルヌーリ分布の中央値はです
-

滝
 すべてを適用します
すべてを適用します
![{displaystyle {tilde {m}}_{X}in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9fd9d909c8c8833e0a4a7b1380b09a8ff318c5) 中央値。
中央値。
カミュレータ [ 編集 | ソーステキストを編集します ]
累積生成関数はです
-
 。
。
最初の累積器も同様です
 再帰方程式が適用されます
再帰方程式が適用されます
-

確率 – 生成関数 [ 編集 | ソーステキストを編集します ]
確率 – 生成関数はです
-
 。
。
特性関数 [ 編集 | ソーステキストを編集します ]
特性関数はです
-
 。
。
モーメント – 生成関数 [ 編集 | ソーステキストを編集します ]
瞬間 – 生成関数はです
-
 。
。
二項分布との関係 [ 編集 | ソーステキストを編集します ]
ベルヌーイの分布は、
 。言い換えれば、同一のパラメーターを備えた独立したベルヌーイと分配されたランダムサイズの合計
。言い換えれば、同一のパラメーターを備えた独立したベルヌーイと分配されたランダムサイズの合計
 二項分布には十分であるため、ベルヌーイの分布は生殖的ではありません。
二項分布には十分であるため、ベルヌーイの分布は生殖的ではありません。
二項分布はそれです
 – 同じパラメーターでベルヌーリ分布の折りたたみ式
– 同じパラメーターでベルヌーリ分布の折りたたみ式
 または同じ確率で
または同じ確率で
 。
。
一般化された二項分布との関係 [ 編集 | ソーステキストを編集します ]
合計
 独立したBernoulliに分配されたランダム変数、これらはすべて異なるパラメーターです
独立したBernoulliに分配されたランダム変数、これらはすべて異なるパラメーターです
 独自は一般化されています。
独自は一般化されています。
ポアソン分布との関係 [ 編集 | ソーステキストを編集します ]
ベルヌーリが分散したランダムサイズの合計は、
 、
、
 と
と

 。これは、合計が二項分布であり、ポアソンアプリケーションが二項分布に適用されるという事実から直接続きます。
。これは、合計が二項分布であり、ポアソンアプリケーションが二項分布に適用されるという事実から直接続きます。
2つのポイント分布との関係 [ 編集 | ソーステキストを編集します ]
ベルヌーイ分布は、2点分布の特別なケースです
 。逆に、2点分布は、ベルヌーリ分布の任意の2要素量への一般化です。
。逆に、2点分布は、ベルヌーリ分布の任意の2要素量への一般化です。
Rademacher分布との関係 [ 編集 | ソーステキストを編集します ]
両方のベルヌーリ分布
 Rademacherの分布と同様に、公正なコインの才能(または公正なランダムなYES/NO決定)のモデリング。唯一の違いは、ヘッド(成功)と数(失敗)が異なるコード化されていることです。
Rademacherの分布と同様に、公正なコインの才能(または公正なランダムなYES/NO決定)のモデリング。唯一の違いは、ヘッド(成功)と数(失敗)が異なるコード化されていることです。
幾何学的分布との関係 [ 編集 | ソーステキストを編集します ]
実験が連続して分配された場合、待ち時間は最初の成功(または定義に応じて最終的な障害)のために幾何学的に分配されます。
離散等分布との関係 [ 編集 | ソーステキストを編集します ]
Bernoulliの分布
 離散等分の分布です
離散等分の分布です
 。
。
urnenmodell [ 編集 | ソーステキストを編集します ]
Bernoulli分布は、urnモデルから生成することもできます。
 は。次に、これはurnからの1つのタイムプルに対応します
は。次に、これはurnからの1つのタイムプルに対応します
 そのボール
そのボール
 赤く、他の誰もが異なる色を持っています。赤いボールを引っ張る可能性は、ベルヌーリに分割されます。
赤く、他の誰もが異なる色を持っています。赤いボールを引っ張る可能性は、ベルヌーリに分割されます。
シミュレーションを使用すると、それを利用してください
 着実に分割されたランダム変数
着実に分割されたランダム変数
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) ランダム変数です
ランダム変数です
 Bernoulliはパラメーターで配布されています
Bernoulliはパラメーターで配布されています
 。ほぼすべてのコンピューターが標準番号を生成できるため、シミュレーションは次のとおりです。
。ほぼすべてのコンピューターが標準番号を生成できるため、シミュレーションは次のとおりです。
- 標準の数を作成します

- は
 、0を与え、それ以外の場合は1を与えます。
、0を与え、それ以外の場合は1を与えます。
これは、反転法に正確に対応します。 Bernoulliで分散したランダム変数の単純なシミュレーションを使用して、二項分布または一般化された二項分散ランダム変数をシミュレートすることもできます。
- ハンス・オットー・ジョージ: Stochastics:確率理論と統計の紹介。 第4版、De Gruyter、2009、ISBN 978-3-11-021526-7。
- ↑ Norbert Kusolitsch: 測定と確率理論 。はじめに。 2番目、改訂版、拡張版。 Springer-Verlag、Berlin Heidelberg 2014、ISBN 978-3-642-45386-1、 S. 63 、doi: 10,1007/978-3-642-45387-8 。
- ↑ クラウスD.シュミット: 測定と確率 。 2番目、エディションを通じて。 Springer-Verlag、Heidelberg Dordrecht London New York 2011、ISBN 978-3-642-21025-9、 S. 254 、doi: 10,1007/978-3-642-21026-6 。
- ↑ ジェームズ・ビクター・ウスペンスキー: 数学的確率の紹介 、McGraw-Hill、ニューヨーク1937、45ページ




 成功のために、成功の確率が呼ばれ、
成功のために、成功の確率が呼ばれ、  故障の確率。
故障の確率。 群衆の中に価値があります
群衆の中に価値があります  それは ゼロワン分布 また。 ベルヌーリの分布 パラメーターで
それは ゼロワン分布 また。 ベルヌーリの分布 パラメーターで ![pin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c) 次の確率関数に従う場合
次の確率関数に従う場合 

 また
また  。
。 
 と
と  該当する:
該当する: 

 したがって
したがって 


 ベルヌーイの分布は、ポイントの周りに対称的にあります
ベルヌーイの分布は、ポイントの周りに対称的にあります  。
。 
 と
と  確率で
確率で  確率で
確率で  。曲がった人のためにそれを手に入れます
。曲がった人のためにそれを手に入れます ![{displaystyle {begin{aligned}operatorname {v} (X)&=operatorname {E} left[left({frac {X-operatorname {E} (X)}{sqrt {operatorname {Var} (X)}}}right)^{3}right]\&=pcdot left({frac {q}{sqrt {pq}}}right)^{3}+qcdot left(-{frac {p}{sqrt {pq}}}right)^{3}\&={frac {1}{{sqrt {pq}}^{3}}}left(pq^{3}-qp^{3}right)\&={frac {pq}{{sqrt {pq}}^{3}}}(q-p)\&={frac {q-p}{sqrt {pq}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/444b272655aba54f608ed51507bd0de15adec89c)


 同じことで、適用されます
同じことで、適用されます 




 すべてを適用します
すべてを適用します ![{displaystyle {tilde {m}}_{X}in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9fd9d909c8c8833e0a4a7b1380b09a8ff318c5) 中央値。
中央値。 
 再帰方程式が適用されます
再帰方程式が適用されます 



 。言い換えれば、同一のパラメーターを備えた独立したベルヌーイと分配されたランダムサイズの合計
。言い換えれば、同一のパラメーターを備えた独立したベルヌーイと分配されたランダムサイズの合計  – 同じパラメーターでベルヌーリ分布の折りたたみ式
– 同じパラメーターでベルヌーリ分布の折りたたみ式  独自は一般化されています。
独自は一般化されています。  、
、  と
と 
 。これは、合計が二項分布であり、ポアソンアプリケーションが二項分布に適用されるという事実から直接続きます。
。これは、合計が二項分布であり、ポアソンアプリケーションが二項分布に適用されるという事実から直接続きます。  。逆に、2点分布は、ベルヌーリ分布の任意の2要素量への一般化です。
。逆に、2点分布は、ベルヌーリ分布の任意の2要素量への一般化です。  Rademacherの分布と同様に、公正なコインの才能(または公正なランダムなYES/NO決定)のモデリング。唯一の違いは、ヘッド(成功)と数(失敗)が異なるコード化されていることです。
Rademacherの分布と同様に、公正なコインの才能(または公正なランダムなYES/NO決定)のモデリング。唯一の違いは、ヘッド(成功)と数(失敗)が異なるコード化されていることです。  離散等分の分布です
離散等分の分布です  は。次に、これはurnからの1つのタイムプルに対応します
は。次に、これはurnからの1つのタイムプルに対応します  そのボール
そのボール  赤く、他の誰もが異なる色を持っています。赤いボールを引っ張る可能性は、ベルヌーリに分割されます。
赤く、他の誰もが異なる色を持っています。赤いボールを引っ張る可能性は、ベルヌーリに分割されます。  着実に分割されたランダム変数
着実に分割されたランダム変数 ![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) ランダム変数です
ランダム変数です  Bernoulliはパラメーターで配布されています
Bernoulliはパラメーターで配布されています 

Recent Comments