
ラウムウィンケル

半径rのボールで
ラウムウィンケル レベルに対して定義された2次元角の3次元の対応物です。 3次元空間全体の割合を記述します。 B.は、特定のボウリングまたはピラミッドコートの中にあります。
空間の角度
 エリアとして定義されます
エリアとして定義されます
 部分領域
部分領域
 半径の正方形で分割された球面表面
半径の正方形で分割された球面表面
 ボール:
ボール:
-
 。
。
ユニットボールを検討するとき(
 ) は
) は
 したがって、同じ量の空間角度。したがって、フルルームの角度はユニットボールの表面に等しくなります。
したがって、同じ量の空間角度。したがって、フルルームの角度はユニットボールの表面に等しくなります。
 。
。
サブエリアは任意のアウトラインにすることができます。ベクトルは、表面積分として書かれています
-
 。
。
ある
 座標ボールトのユニットベクトル、
座標ボールトのユニットベクトル、
 微分領域要素と
微分領域要素と
 座標起点からの距離。
座標起点からの距離。
写真とは異なり、エリアのアウトラインは役割を果たしません。同じ領域のボール表面の各アウトラインは、同じサイズのスペース角を定義します。ボールの中心がアウトラインの各ポイントを通る出発点としてビームを配置すると、スペース角を示す幾何学的な人物が得られます。これは、レベルの角度のディスプレイに匹敵します。2つのセミストレートが共通の出発点です。
空間の角度は寸法数のサイズですが、主にSteradiant(SR)ユニットに示されています。これは、平らな角度の放射(ホイール)ユニットを使用したアーチサイズに対応します。 1 SRの室内角度は、半径1 mのボール上の1 mの面積を囲みます 2 。球面全体の面から領域
 関連するフルスペース角があります
関連するフルスペース角があります
-
 。
。
時折、スペース角も正方形(°)²で与えられます。 1(°)²は同じです
 。
。
寸法のサイズに補助ユニットを使用するには、多くの領域、特に空間角度のように、使用されるユニットからすでに見られるという利点があります。光の流れ(LM)とは対照的に、光強度(CD = LM/SR)は、ユニット内のsteradiantが発生しているため、空間角への依存性を示しています。したがって、光強度は、空間角に依存する光流れを表します。

デカルト極座標セクションからの部屋の角度
ボールの三角形の空間角は、その内側の角度に依存しています
 steradiant(参照 バグトライアングル – プロパティ )。
steradiant(参照 バグトライアングル – プロパティ )。
球状座標系では、放射状変数がないため、空間角を特に明確に定義できます。 2つの子午線角
 、
、
 および2つの幅の角度
および2つの幅の角度
 、
、
 球面上の面積要素を決定します。関連する空間角度は次のとおりです。
球面上の面積要素を決定します。関連する空間角度は次のとおりです。
-

ボールの表面のアウトラインとして円を選択すると、正規の空間角が得られます。スペース角は、ボールの中心がある上部にまっすぐな円錐のコートを形成します。
は
 コーンの先端の開口角度、次にスペース角度が生じます
コーンの先端の開口角度、次にスペース角度が生じます
 二重積分から [初め]
二重積分から [初め]


開口角
 卒業生 卒業生 |
0 |
初め |
2 |
5 |
十 |
15 |
30 |
45 |
57,2958 |
開口角
 放射で 放射で |
0.0000 |
0.0175 |
0.0349 |
0.0873 |
0.1745 |
0.2618 |
0.5236 |
0.7854 |
1.0000 |
ラウムウィンケル
 Quadratgradで Quadratgradで |
0.00 |
0.79 |
3.14 |
19.63 |
78.49 |
176.46 |
702.83 |
1570,10 |
2525.04 |
ラウムウィンケル
 steradiantで steradiantで |
0.0000 |
0.0002 |
0.0010 |
0.0060 |
0.0239 |
0.0538 |
0.2141 |
0.4783 |
0.7692 |
| |
開口角
 卒業生 卒業生 |
60 |
65,5411 |
75 |
90 |
120 |
150 |
180 |
270 |
360 |
開口角
 放射で 放射で |
1,0472 |
1.1439 |
1,3090 |
1,5708 |
2.0944 |
2,6180 |
3.1416 |
4,7124 |
6,2832 |
ラウムウィンケル
 Quadratgradで Quadratgradで |
2763.42 |
3282.81 |
4262,39 |
6041.36 |
10313.24 |
15287.95 |
20626,48 |
35211.60 |
41252,96 |
ラウムウィンケル
 steradiantで steradiantで |
0.8418 |
1.0000 |
1.2984 |
1.8403 |
3.1416 |
4,6570 |
6,2832 |
10,7261 |
12,5664 |
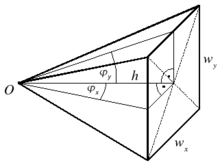
ピラミッドの空間に
長方形および平らなアウトラインを備えた空間角の特殊なケースは、ピラミッドの幾何学的形状に対応します。これにより、原点はレベル長方形の中心上に正確に垂直です(図を参照)。この空間角度はzになります。 B.長方形の開口部を使用して光学システムのétendueを計算する場合。
OosteromとStrackeの式で非常に簡単に計算できます。ピラミッドページ付き
 と
と
 高さと同様に h 降伏:
高さと同様に h 降伏:
-

計算に2つの開口角を使用する場合
 と
と
 、それによって
、それによって
 と
と
 いくつかの三角変換が続きます:
いくつかの三角変換が続きます:
-

例:
点光源の前の長方形のカバーは、角度45°(
 )および20°(
)および20°(
 )a。スペース角は0.27 Srです。
)a。スペース角は0.27 Srです。
正方形の開口部であり、両方の角度がサイズが20°の場合、スペース角には0.12 SRが含まれます。 20°円のパネルの標準空間角は0.10 srです。
スペース角の3式 [ 編集 | ソーステキストを編集します ]
以下には
 ベクトルを4ポイント
ベクトルを4ポイント
 1つのレベルではありません(部屋を固定します)、
1つのレベルではありません(部屋を固定します)、
 周りの均一なボールです
周りの均一なボールです
 と
と
 ストレートの交差点
ストレートの交差点
 ユニットボールで
ユニットボールで
 。
。
 四面体を形成します。
四面体を形成します。

角に単一のボールが付いたキューブ
レイヤー式 [ 編集 | ソーステキストを編集します ]
ショップ
 球形の三角形の
球形の三角形の
 3つの間の角度です レベル それは3つのポイントトリプルを通して
3つの間の角度です レベル それは3つのポイントトリプルを通して
 、
、
 、
、
 クランプされる。
クランプされる。
球形の三角形の面積
 四面体の角の室内角度です
四面体の角の室内角度です
 (上記を参照):
(上記を参照):
 。
。
例: ために
 角度です
角度です
 ゼロポイントのスペース角
ゼロポイントのスペース角
-

エッジフォーミュラ [ 編集 | ソーステキストを編集します ]
がある
 3つの直線の間の角度
3つの直線の間の角度
 。それらが含まれています レース ポイントの四面体の
。それらが含まれています レース ポイントの四面体の
 。
。
その後、空間角度は、l’uilierの文で計算できます。 [2]
 。
。
例: ために
 角度です
角度です
 と
と
-
 。
。
ポイント内の空間の角度
 (前と同じ)同じです
(前と同じ)同じです
 。
。
方向ベクトル式 [ 編集 | ソーステキストを編集します ]
ベクトルです
 ストレートの方向ベクトル
ストレートの方向ベクトル
 したがって、宇宙角に適用されます
したがって、宇宙角に適用されます
 。
。
ある
 ベクターのスパー積
ベクターのスパー積
 、
、
 と
と
 、
、
 スカラー製品です
スカラー製品です
 ベクトルの長さです。
ベクトルの長さです。
このプレゼンテーションは、1983年にOosteromとStrackeによって行われました [3] 指定および実証済み。
例: ために
 それは
それは
 方向ベクター。と
方向ベクター。と
 ために
ために
 結果(上記のように)
結果(上記のように)
-

角に3つのエッジがある例 [ 編集 | ソーステキストを編集します ]
空間角を決定するための3つの式は、3つのエッジ(レベル)を持つすべてのポリホラーに適用できます。
通常の四面体 [ 編集 | ソーステキストを編集します ]
通常の四面体で、側面間の角度は
 そして、レイヤー式の後
そして、レイヤー式の後
-

エッジアングルはです
 そして、それはエッジフォーミュラに従って適用されます
そして、それはエッジフォーミュラに従って適用されます
-

Gerades Prisma [ 編集 | ソーステキストを編集します ]
ストレートプリズムには、ベースエリアとしてN_CCKがあり、床面積垂直方向の他のエッジ(レベル)があります。 1つのポイントの角度です
 基本エリアポリゴンの
基本エリアポリゴンの
 これに続いて、空間角度の側面の直交性のためにレイヤー式(上記参照)が続きます
これに続いて、空間角度の側面の直交性のためにレイヤー式(上記参照)が続きます

-
 。
。
オクタヘダーの切り株 [ 編集 | ソーステキストを編集します ]
八面体の切り株は、通常の八面体の割礼によって作成されます。隅に
 3つのエッジと3つのレベル、2つの通常の六角形と正方形に会います。したがって、2つの領域があります。
3つのエッジと3つのレベル、2つの通常の六角形と正方形に会います。したがって、2つの領域があります。
 2つの六角形の間と
2つの六角形の間と
 六角形と正方形の間。適用されます(Octaheder Stumpを参照)
六角形と正方形の間。適用されます(Octaheder Stumpを参照)
-

上記のレベルの式によると、空間角度はポイントにあります


オクタヘダーの切り株の角のスペース角度は同じです
 フルスペースアングルの。この結果は、3次元のユークリッド空間を一致するオクタヘダーの切り株で完全に記入できるという事実によって確認されています。 部屋の詰め物 )。
フルスペースアングルの。この結果は、3次元のユークリッド空間を一致するオクタヘダーの切り株で完全に記入できるという事実によって確認されています。 部屋の詰め物 )。
隅により多くのエッジがある例 [ 編集 | ソーステキストを編集します ]
3つ以上のエッジがポリダーコーナーを通過する場合、3つ以上の角を持つ球状ポリゴンがあります。多くの場合、球形ポリゴンは、内側の補助ポイントの助けを借りて使用できます
 球形の三角形にブラシをかけます(平らな凸ポリゴンの三角測量に類似)。
球形の三角形にブラシをかけます(平らな凸ポリゴンの三角測量に類似)。
特に四角いピラミッド [ 編集 | ソーステキストを編集します ]

特に四角いピラミッド:宇宙角計算のために上部で分解
正方形の側面を持つまっすぐな正方形のピラミッドの場合
 と高さ
と高さ
 三角形間の角度です
三角形間の角度です
-

ケーキから、ピラミッドの高さに沿って、2つの隣接する基底ポイントなどのピラミッドを切り取ると、ベースに三角形の床領域とピラミッドの縁があるピラミッドが得られます。三角形のピラミッドの上部にある空間の角度には、次のようになります。
-

-

そして、ピラミッドの宇宙角が一番上にあります

三角形と正方形の間の角度はです
-

レイヤーフォーミュラを使用すると、スペース角度のベースコーナーになります

-

特別:
ために
 ピラミッドのものです ハーフオクタイヘダー 。この場合、スペース角は上部にあります
ピラミッドのものです ハーフオクタイヘダー 。この場合、スペース角は上部にあります
-
 。
。
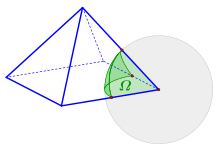
四角いピラミッド:半分のオクタイザー
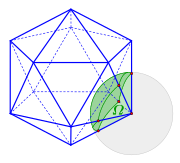
Ikosaeder、Raumwinkel

通常のIkosaeder [ 編集 | ソーステキストを編集します ]
ここで説明する方法は、通常のIkosaederのスペース角を決定する際にも使用されます。 Ikosaederを使用すると、5つのエッジが各コーナーを通過します。通常の五角形を備えたピラミッドの宇宙角は、ベースとして決定されます。
- ↑ オレグ・マゾンカ: 円錐表面、多面体コーン、および交差する球状キャップの元角度
- ↑ Wolfram Mathworld: 球状の過剰
- ↑ A.ヴァン・オステルム、J。ストラッキー: 平面三角形の元角 。の: 生物医学工学、IEEE取引 。 BME-30、 いいえ。 2 、1983年、 S. 125–126 、doi: 10.1109/tbme.1983.325207 。


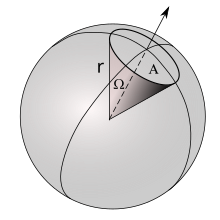










 エリアとして定義されます
エリアとして定義されます  部分領域
部分領域  半径の正方形で分割された球面表面
半径の正方形で分割された球面表面  ボール:
ボール: 
 ) は
) は  。
。 
 座標ボールトのユニットベクトル、
座標ボールトのユニットベクトル、  微分領域要素と
微分領域要素と  関連するフルスペース角があります
関連するフルスペース角があります 
 。
。  steradiant(参照 バグトライアングル – プロパティ )。
steradiant(参照 バグトライアングル – プロパティ )。  、
、  および2つの幅の角度
および2つの幅の角度  、
、  球面上の面積要素を決定します。関連する空間角度は次のとおりです。
球面上の面積要素を決定します。関連する空間角度は次のとおりです。 
 コーンの先端の開口角度、次にスペース角度が生じます
コーンの先端の開口角度、次にスペース角度が生じます 
 と
と  高さと同様に h 降伏:
高さと同様に h 降伏: 
 と
と  、それによって
、それによって  と
と  いくつかの三角変換が続きます:
いくつかの三角変換が続きます: 
 )および20°(
)および20°(  )a。スペース角は0.27 Srです。
)a。スペース角は0.27 Srです。  ベクトルを4ポイント
ベクトルを4ポイント  1つのレベルではありません(部屋を固定します)、
1つのレベルではありません(部屋を固定します)、  周りの均一なボールです
周りの均一なボールです  と
と  ストレートの交差点
ストレートの交差点  ユニットボールで
ユニットボールで  球形の三角形の
球形の三角形の  、
、  、
、  クランプされる。
クランプされる。 
 角度です
角度です  ゼロポイントのスペース角
ゼロポイントのスペース角 
 3つの直線の間の角度
3つの直線の間の角度 
 と
と 
 。
。  ストレートの方向ベクトル
ストレートの方向ベクトル 
 ベクターのスパー積
ベクターのスパー積  、
、  と
と  、
、  スカラー製品です
スカラー製品です  ベクトルの長さです。
ベクトルの長さです。  方向ベクター。と
方向ベクター。と  ために
ために  結果(上記のように)
結果(上記のように) 
 そして、レイヤー式の後
そして、レイヤー式の後 
 そして、それはエッジフォーミュラに従って適用されます
そして、それはエッジフォーミュラに従って適用されます 
 基本エリアポリゴンの
基本エリアポリゴンの  これに続いて、空間角度の側面の直交性のためにレイヤー式(上記参照)が続きます
これに続いて、空間角度の側面の直交性のためにレイヤー式(上記参照)が続きます 
 2つの六角形の間と
2つの六角形の間と  六角形と正方形の間。適用されます(Octaheder Stumpを参照)
六角形と正方形の間。適用されます(Octaheder Stumpを参照) 

 フルスペースアングルの。この結果は、3次元のユークリッド空間を一致するオクタヘダーの切り株で完全に記入できるという事実によって確認されています。 部屋の詰め物 )。
フルスペースアングルの。この結果は、3次元のユークリッド空間を一致するオクタヘダーの切り株で完全に記入できるという事実によって確認されています。 部屋の詰め物 )。  球形の三角形にブラシをかけます(平らな凸ポリゴンの三角測量に類似)。
球形の三角形にブラシをかけます(平らな凸ポリゴンの三角測量に類似)。  と高さ
と高さ  三角形間の角度です
三角形間の角度です 






 ピラミッドのものです ハーフオクタイヘダー 。この場合、スペース角は上部にあります
ピラミッドのものです ハーフオクタイヘダー 。この場合、スペース角は上部にあります 
Recent Comments