Ising Modell – Wikipedia

Mathematisches Modell des Ferromagnetismus in der statistischen Mechanik

Das Ising Modell (; Deutsche: [ˈiːzɪŋ]), benannt nach dem Physiker Ernst Ising, ist ein mathematisches Modell des Ferromagnetismus in der statistischen Mechanik. Das Modell besteht aus diskreten Variablen, die magnetische Dipolmomente von Atomen darstellen “dreht sich” das kann in einem von zwei Zuständen sein (+1 oder −1). Die Drehungen sind in einem Diagramm angeordnet, normalerweise in einem Gitter (wobei sich die lokale Struktur periodisch in alle Richtungen wiederholt), sodass jede Drehung mit ihren Nachbarn interagieren kann. Übereinstimmende benachbarte Drehungen haben eine geringere Energie als nicht übereinstimmende. Das System tendiert zur niedrigsten Energie, aber Wärme stört diese Tendenz und schafft so die Möglichkeit unterschiedlicher Strukturphasen. Das Modell ermöglicht die Identifizierung von Phasenübergängen als vereinfachtes Modell der Realität. Das zweidimensionale Ising-Modell mit quadratischem Gitter ist eines der einfachsten statistischen Modelle zur Darstellung eines Phasenübergangs.^[1]

Das Ising-Modell wurde vom Physiker Wilhelm Lenz (1920) erfunden, der es seinem Schüler Ernst Ising als Problem gab. Das eindimensionale Ising-Modell wurde von Ising (1925) selbst in seiner Arbeit von 1924 gelöst;^[2] es hat keinen Phasenübergang. Das zweidimensionale Ising-Modell mit quadratischem Gitter ist viel schwieriger und wurde erst viel später von Lars Onsager (1944) analytisch beschrieben. Es wird normalerweise durch eine Transfermatrixmethode gelöst, obwohl es verschiedene Ansätze gibt, die eher mit der Quantenfeldtheorie zusammenhängen.

Bei Dimensionen größer als vier wird der Phasenübergang des Ising-Modells durch die mittlere Feldtheorie beschrieben.

Das Modell selbst ist ein mittleres Feldmodell, dh die Interaktion zwischen zwei beliebigen Spins ist ungefähr unabhängig von den räumlichen Positionen dieser Spins. Diese Annahme wird auferlegt, um das Studium des Modells zu vereinfachen. Es stellt sich heraus, dass das Modell weitaus schwieriger zu untersuchen ist, wenn man stattdessen die räumlichen Orte einbeziehen möchte (über einen Spin-Spin-Interaktionsparameter, der beispielsweise mit zunehmendem Abstand zwischen den Spins abnimmt). Dies rechtfertigt die oben erwähnte vereinfachende Annahme, insbesondere angesichts der Tatsache, dass die strengen mathematischen Ergebnisse zu diesem Modell erst vor kurzem vorliegen.^[3]

Das Ising-Problem ohne externes Feld kann äquivalent als Graph-Maximum-Cut-Problem (Max-Cut) formuliert werden, das durch kombinatorische Optimierung gelöst werden kann.

Definition[edit]

Betrachten Sie eine Menge Λ von Gitterplätzen, von denen jede einen Satz benachbarter Stellen (z. B. einen Graphen) bildet d-dimensionales Gitter. Für jede Gitterstelle k ∈ ∈ es gibt eine diskrete Variable σ_k so dass σ_k ∈ {+1, −1}, repräsentiert den Spin der Site. EIN Spin-Konfiguration, σ = (σ_k)_{k ∈ ∈} ist eine Zuordnung des Spinwerts zu jeder Gitterstelle.

Für zwei beliebige benachbarte Standorte ich, j ∈ ∈ da ist ein Interaktion J._ij. Auch eine Seite j ∈ ∈ hat eine externes Magnetfeld h_j damit interagieren. Das Energie einer Konfiguration σ ist durch die Hamilton-Funktion gegeben

${ displaystyle H ( sigma) = – sum _ { langle i ~ j rangle} J_ {ij} sigma _ {i} sigma _ {j} – mu sum _ {j} h_ {j } sigma _ {j},}$

Dabei liegt die erste Summe über Paaren benachbarter Spins (jedes Paar wird einmal gezählt). Die Notation ⟨ij⟩ Zeigt an, dass Websites ich und j sind nächste Nachbarn. Das magnetische Moment ist gegeben durch µ. Es ist zu beachten, dass das Vorzeichen im zweiten Term des obigen Hamilton-Operators tatsächlich positiv sein sollte, da das magnetische Moment des Elektrons antiparallel zu seinem Spin ist, der negative Term jedoch konventionell verwendet wird.^[4] Das Konfigurationswahrscheinlichkeit ist gegeben durch die Boltzmann-Verteilung mit inverser Temperatur β ≥ 0:

${ displaystyle P _ { beta} ( sigma) = { frac {e ^ {- beta H ( sigma)}} {Z _ { beta}}},}$

wobei β = (k_B.T.)⁻¹und die Normalisierungskonstante

${ displaystyle Z _ { beta} = sum _ { sigma} e ^ {- beta H ( sigma)}}$

ist die Partitionsfunktion. Für eine Funktion f der Spins (“beobachtbar”) bezeichnet man mit

${ displaystyle langle f rangle _ { beta} = sum _ { sigma} f ( sigma) P _ { beta} ( sigma)}$

der Erwartungswert (Mittelwert) von f.

Die Konfigurationswahrscheinlichkeiten P._β(σ) stellen die Wahrscheinlichkeit dar, dass sich das System (im Gleichgewicht) in einem Zustand mit der Konfiguration σ befindet.

Diskussion[edit]

Das Minuszeichen für jeden Term der Hamilton-Funktion H.(σ) ist konventionell. Unter Verwendung dieser Vorzeichenkonvention können Ising-Modelle nach dem Vorzeichen der Interaktion klassifiziert werden: wenn für ein Paar ich, j

${ displaystyle J_ {ij}> 0}$

${ displaystyle J_ {ij} <0}$

wird die Wechselwirkung als antiferromagnetisch bezeichnet,

${ displaystyle J_ {ij} = 0}$

sind die Spins nicht wechselwirkend.

Das System wird als ferromagnetisch oder antiferromagnetisch bezeichnet, wenn alle Wechselwirkungen ferromagnetisch oder alle antiferromagnetisch sind. Die ursprünglichen Ising-Modelle waren ferromagnetisch, und es wird immer noch oft angenommen, dass “Ising Modell” bedeutet ein ferromagnetisches Ising-Modell.

In einem ferromagnetischen Ising-Modell möchten Spins ausgerichtet werden: Die Konfigurationen, bei denen benachbarte Spins das gleiche Vorzeichen haben, haben eine höhere Wahrscheinlichkeit. In einem antiferromagnetischen Modell neigen benachbarte Spins dazu, entgegengesetzte Vorzeichen zu haben.

Die Zeichenkonvention von H.(σ) erklärt auch, wie eine Spinstelle j interagiert mit dem externen Feld. Die Spinstelle möchte nämlich mit dem externen Feld ausgerichtet sein. Wenn:

${ displaystyle h_ {j}> 0}$

${ displaystyle h_ {j} <0}$

, die Spinstelle j wünscht sich in die negative Richtung auszurichten,

${ displaystyle h_ {j} = 0}$

gibt es keinen äußeren Einfluss auf die Spinstelle.

Vereinfachungen[edit]

Ising-Modelle werden häufig untersucht, ohne dass ein externes Feld mit dem Gitter interagiert, d. H. h = 0 für alle j im Gitter Λ. Mit dieser Vereinfachung wird der Hamiltonianer

${ displaystyle H ( sigma) = – sum _ { langle i ~ j rangle} J_ {ij} sigma _ {i} sigma _ {j}.}$

Wenn das externe Feld überall Null ist, h = 0, das Ising-Modell ist symmetrisch, wenn der Wert des Spins an allen Gitterplätzen umgeschaltet wird; Ein Feld ungleich Null unterbricht diese Symmetrie.

Eine weitere häufige Vereinfachung ist die Annahme, dass alle nächsten Nachbarn ⟨ij⟩ Haben die gleiche Wechselwirkungsstärke. Dann können wir einstellen J._ij = J. für alle Paare ich, j in Λ. In diesem Fall wird der Hamilton-Operator weiter vereinfacht

${ displaystyle H ( sigma) = – J sum _ { langle i ~ j rangle} sigma _ {i} sigma _ {j}.}$

Verbindung zum maximalen Schnitt des Diagramms[edit]

Eine Teilmenge S der Scheitelpunktmenge V (G) eines gewichteten ungerichteten Graphen G bestimmt einen Schnitt des Graphen G in S und seine komplementäre Teilmenge G S. Die Größe des Schnitts ist die Summe der Gewichte der Kanten zwischen S und G S. Eine maximale Schnittgröße ist mindestens die Größe eines anderen Schnitts und variiert S.

Für das Ising-Modell ohne externes Feld in einem Graphen G wird der Hamilton-Operator die folgende Summe über den Graphenkanten E (G)

${ displaystyle H ( sigma) = – sum _ {ij in E (G)} J_ {ij} sigma _ {i} sigma _ {j}}$

.

Hier ist jeder Scheitelpunkt i des Graphen eine Spinstelle, die einen Spinwert annimmt

${ displaystyle sigma _ {i} = pm 1}$

. Eine gegebene Spin-Konfiguration

${ displaystyle sigma}$

partitioniert die Menge der Eckpunkte

${ displaystyle V (G)}$

in zwei

${ displaystyle sigma}$

-abhängige Untergruppen, solche mit Spin-up

${ displaystyle V ^ {+}}$

und diejenigen mit Spin-Down

${ displaystyle V ^ {-}}$

. Wir bezeichnen mit

${ displaystyle delta (V ^ {+})}$

das

${ displaystyle sigma}$

-abhängige Menge von Kanten, die die beiden komplementären Scheitelpunkt-Teilmengen verbindet

${ displaystyle V ^ {+}}$

und

${ displaystyle V ^ {-}}$

. Das Größe

${ displaystyle left | delta (V ^ {+}) right |}$

des Schnitts

${ displaystyle delta (V ^ {+})}$

um zweiteilig zu sein, kann der gewichtete ungerichtete Graph G definiert werden als

${ displaystyle left | delta (V ^ {+}) right | = { frac {1} {2}} sum _ {ij in delta (V ^ {+})} W_ {ij} }}$

,

wo

${ displaystyle W_ {ij}}$

bezeichnet ein Gewicht der Kante

${ displaystyle ij}$

und die Skalierung 1/2 wird eingeführt, um die Doppelzählung der gleichen Gewichte zu kompensieren

${ displaystyle W_ {ij} = W_ {ji}}$

.

Die Identitäten

${ displaystyle { begin {align} H ( sigma) & = – sum _ {ij in E (V ^ {+})} J_ {ij} – sum _ {ij in E (V ^ { -})} J_ {ij} + sum _ {ij in delta (V ^ {+})} J_ {ij} \ & = – sum _ {ij in E (G)} J_ {ij } +2 sum _ {ij in delta (V ^ {+})} J_ {ij}, end {align}}}$

wobei die Gesamtsumme im ersten Term nicht davon abhängt

${ displaystyle sigma}$

implizieren, dass die Minimierung

${ displaystyle H ( sigma)}$

im

${ displaystyle sigma}$

ist gleichbedeutend mit Minimierung

${ displaystyle sum _ {ij in delta (V ^ {+})} J_ {ij}}$

. Kantengewicht definieren

${ displaystyle W_ {ij} = – J_ {ij}}$

Auf diese Weise wird das Ising-Problem ohne externes Feld in ein Diagramm-Max-Cut-Problem umgewandelt
^[5] Maximierung der Schnittgröße

${ displaystyle left | delta (V ^ {+}) right |}$

, der wie folgt mit dem Ising Hamiltonian verwandt ist,

${ displaystyle H ( sigma) = sum _ {ij in E (G)} W_ {ij} -4 left | delta (V ^ {+}) right |.}$

Fragen[edit]

Eine signifikante Anzahl statistischer Fragen zu diesem Modell befindet sich an der Grenze einer großen Anzahl von Drehungen:

• Sind in einer typischen Konfiguration die meisten Drehungen +1 oder -1 oder sind sie gleichmäßig aufgeteilt?
• Wenn ein Spin an einer bestimmten Position ich ist 1, was ist die Wahrscheinlichkeit, dass sich der Spin an der Position befindet j ist auch 1?
• Wenn β geändert wird, gibt es einen Phasenübergang?
• Was ist auf einem Gitter Λ die fraktale Dimension der Form eines großen Clusters von +1 Spins?

Grundlegende Eigenschaften und Geschichte[edit]

Der am besten untersuchte Fall des Ising-Modells ist das translatorisch-invariante ferromagnetische Nullfeldmodell auf a d-dimensionales Gitter, nämlich Λ = Z.^d, J._ij = 1, h = 0.

In seiner Doktorarbeit von 1924 löste Ising das Modell für die d = 1 Fall, der als lineares horizontales Gitter betrachtet werden kann, bei dem jeder Ort nur mit seinem linken und rechten Nachbarn interagiert. In einer Dimension lässt die Lösung keinen Phasenübergang zu.^[6] Für jedes positive β sind nämlich die Korrelationen ⟨σ_ichσ_j⟩ Zerfällt exponentiell in |ich – – j|:

${ displaystyle langle sigma _ {i} sigma _ {j} rangle _ { beta} leq C exp { big (} -c ( beta) | ij | { big)},}$

und das System ist ungeordnet. Aufgrund dieses Ergebnisses gelangte er fälschlicherweise zu dem Schluss, dass dieses Modell in keiner Dimension ein Phasenverhalten aufweist.

Das Ising-Modell durchläuft einen Phasenübergang zwischen einer geordneten und einer ungeordneten Phase in zwei oder mehr Dimensionen. Das System ist nämlich für kleines β ungeordnet, während das System für großes β eine ferromagnetische Ordnung aufweist:

${ displaystyle langle sigma _ {i} sigma _ {j} rangle _ { beta} geq c ( beta)> 0.}$

[7] mit dem, was jetzt a genannt wird Peierls Argument.

Das Ising-Modell auf einem zweidimensionalen quadratischen Gitter ohne Magnetfeld wurde von Lars Onsager (1944) analytisch gelöst. Onsager zeigte, dass die Korrelationsfunktionen und die freie Energie des Ising-Modells durch eine nicht wechselwirkende Gitterfermion bestimmt werden. Onsager kündigte 1949 die Formel für die spontane Magnetisierung des zweidimensionalen Modells an, gab jedoch keine Ableitung. Yang (1952) gab den ersten veröffentlichten Beweis für diese Formel unter Verwendung einer Grenzformel für Fredholm-Determinanten, die Szegő 1951 als direkte Reaktion auf Onsagers Arbeit bewies.^[8]

Historische Bedeutung[edit]

Eines der Argumente von Demokrit zur Unterstützung des Atomismus war, dass Atome auf natürliche Weise die scharfen Phasengrenzen erklären, die in Materialien beobachtet werden^{[citation needed]}, wie wenn Eis zu Wasser schmilzt oder Wasser zu Dampf wird. Seine Idee war, dass kleine Änderungen der Eigenschaften auf atomarer Ebene zu großen Änderungen des Aggregatverhaltens führen würden. Andere glaubten, dass Materie von Natur aus kontinuierlich und nicht atomar ist und dass die Eigenschaften der Materie im großen Maßstab nicht auf grundlegende atomare Eigenschaften reduziert werden können.

Während die Gesetze der chemischen Bindung den Chemikern des 19. Jahrhunderts klar machten, dass Atome real waren, wurde die Debatte unter Physikern bis weit in das frühe 20. Jahrhundert hinein fortgesetzt. Atomisten, insbesondere James Clerk Maxwell und Ludwig Boltzmann, wandten Hamiltons Formulierung der Newtonschen Gesetze auf große Systeme an und stellten fest, dass das statistische Verhalten der Atome Gase bei Raumtemperatur korrekt beschreibt. Die klassische statistische Mechanik berücksichtigte jedoch nicht alle Eigenschaften von Flüssigkeiten und Feststoffen sowie von Gasen bei niedriger Temperatur.

Nach der Formulierung der modernen Quantenmechanik stand der Atomismus nicht mehr im Widerspruch zum Experiment, was jedoch nicht zu einer universellen Akzeptanz der statistischen Mechanik führte, die über den Atomismus hinausging. Josiah Willard Gibbs hatte einen vollständigen Formalismus gegeben, um die Gesetze der Thermodynamik aus den Gesetzen der Mechanik zu reproduzieren. Viele fehlerhafte Argumente blieben jedoch aus dem 19. Jahrhundert erhalten, als die statistische Mechanik als zweifelhaft angesehen wurde. Die Fehler in der Intuition resultierten hauptsächlich aus der Tatsache, dass die Grenze eines unendlichen statistischen Systems viele Null-Eins-Gesetze hat, die in endlichen Systemen fehlen: Eine infinitesimale Änderung eines Parameters kann zu großen Unterschieden im gesamten aggregierten Verhalten führen, wie Demokrit erwartet.

Keine Phasenübergänge im endlichen Volumen[edit]

Zu Beginn des 20. Jahrhunderts glaubten einige, dass die Partitionsfunktion niemals einen Phasenübergang beschreiben könne, basierend auf dem folgenden Argument:

1. Die Partitionsfunktion ist eine Summe von e^−βE. über alle Konfigurationen.
2. Die Exponentialfunktion ist überall als Funktion von β analytisch.
3. Die Summe der analytischen Funktionen ist eine analytische Funktion.

Dieses Argument funktioniert für eine endliche Summe von Exponentialen und stellt korrekt fest, dass die freie Energie eines Systems endlicher Größe keine Singularitäten enthält. Bei Systemen, die sich im thermodynamischen Grenzbereich befinden (dh bei unendlichen Systemen), kann die unendliche Summe zu Singularitäten führen. Die Konvergenz zur thermodynamischen Grenze ist schnell, so dass das Phasenverhalten bereits auf einem relativ kleinen Gitter erkennbar ist, obwohl die Singularitäten durch die endliche Größe des Systems geglättet werden.

Dies wurde erstmals von Rudolf Peierls im Ising-Modell festgestellt.

Peierls Tröpfchen[edit]

Kurz nachdem Lenz und Ising das Ising-Modell konstruiert hatten, konnte Peierls explizit zeigen, dass ein Phasenübergang in zwei Dimensionen stattfindet.

Dazu verglich er die Grenzwerte für hohe und niedrige Temperaturen. Bei unendlicher Temperatur (β = 0) haben alle Konfigurationen die gleiche Wahrscheinlichkeit. Jeder Spin ist völlig unabhängig von jedem anderen. Wenn typische Konfigurationen bei unendlicher Temperatur so dargestellt werden, dass Plus / Minus durch Schwarzweiß dargestellt werden, sehen sie wie Fernsehschnee aus. Bei hohen, aber nicht unendlichen Temperaturen gibt es kleine Korrelationen zwischen benachbarten Positionen, der Schnee neigt dazu, ein wenig zu verklumpen, aber der Bildschirm bleibt zufällig und es gibt keinen Nettoüberschuss an Schwarz oder Weiß.

Ein quantitatives Maß für den Überschuss ist das Magnetisierung, das ist der Durchschnittswert des Spins:

${ displaystyle M = { frac {1} {N}} sum _ {i = 1} ^ {N} sigma _ {i}.}$

Ein falsches Argument analog zum Argument im letzten Abschnitt stellt nun fest, dass die Magnetisierung im Ising-Modell immer Null ist.

1. Jede Konfiguration von Spins hat die gleiche Energie wie die Konfiguration, bei der alle Spins umgedreht sind.
2. Also für jede Konfiguration mit Magnetisierung M. Es gibt eine Konfiguration mit Magnetisierung –M. mit gleicher Wahrscheinlichkeit.
3. Das System sollte daher gleich viel Zeit in der Konfiguration mit Magnetisierung verbringen M. wie bei der Magnetisierung –M..
4. Die durchschnittliche Magnetisierung (über alle Zeiten) ist also Null.

Dies beweist nach wie vor nur, dass die durchschnittliche Magnetisierung bei jedem endlichen Volumen Null ist. Bei einem unendlichen System können Schwankungen das System möglicherweise nicht mit einer Wahrscheinlichkeit ungleich Null von einem Zustand mit größtenteils Plus auf einen Zustand mit größtenteils Minus verschieben.

Bei sehr hohen Temperaturen ist die Magnetisierung Null, da sie bei unendlicher Temperatur liegt. Um dies zu sehen, ist zu beachten, dass, wenn Spin A nur eine geringe Korrelation ε mit Spin B aufweist und B nur schwach mit C korreliert, C jedoch ansonsten unabhängig von A ist, der Korrelationsbetrag von A und C wie ε verläuft². Für zwei durch Abstand getrennte Drehungen L.beträgt der Korrelationsbetrag ε^L.Wenn es jedoch mehr als einen Pfad gibt, auf dem sich die Korrelationen bewegen können, wird dieser Betrag um die Anzahl der Pfade erhöht.

Die Anzahl der Längenpfade L. auf einem quadratischen Gitter in d Abmessungen ist

${ displaystyle N (L) = (2d) ^ {L},}$

da gibt es 2d Auswahlmöglichkeiten für jeden Schritt.

Eine Grenze für die Gesamtkorrelation ergibt sich aus dem Beitrag zur Korrelation durch Summieren über alle Pfade, die zwei Punkte verbinden, was oben durch die Summe über alle Pfade der Länge begrenzt ist L. geteilt durch

${ displaystyle sum _ {L} (2d) ^ {L} varepsilon ^ {L},}$

was auf Null geht, wenn ε klein ist.

Bei niedrigen Temperaturen (β ≫ 1) liegen die Konfigurationen in der Nähe der Konfiguration mit der niedrigsten Energie, bei der alle Spins plus oder alle Spins minus sind. Peierls fragte, ob es statistisch möglich ist, bei niedriger Temperatur, beginnend mit allen Drehungen minus, in einen Zustand zu schwanken, in dem die meisten Drehungen plus sind. Dazu müssen Tröpfchen von Plus-Spin erstarren können, um den Plus-Zustand zu erreichen.

Die Energie eines Tröpfchens von Plus-Drehungen in einem Minus-Hintergrund ist proportional zum Umfang des Tröpfchens L, wobei Plus-Drehungen und Minus-Drehungen nebeneinander liegen. Für ein Tröpfchen mit Umfang L.liegt der Bereich irgendwo zwischen (L. – 2) / 2 (die gerade Linie) und (L./ 4)² (die quadratische Box). Die Wahrscheinlichkeitskosten für das Einbringen eines Tropfens haben den Faktor e^−βL.Dies trägt jedoch zur Partitionsfunktion multipliziert mit der Gesamtzahl der Tröpfchen mit Umfang bei L.Dies ist weniger als die Gesamtzahl der Pfade mit einer Länge L.::

${ displaystyle N (L) <4 ^ {2L}.}$

Damit ist der gesamte Spinbeitrag von Tröpfchen, selbst wenn er überzählt wird, indem jeder Stelle ein separates Tröpfchen zugewiesen wird, oben durch begrenzt

${ displaystyle sum _ {L} L ^ {2} 4 ^ {2L} e ^ {- 4 beta L},}$

das geht auf Null bei großen β. Für ausreichend großes β unterdrückt dies exponentiell lange Schleifen, so dass sie nicht auftreten können und die Magnetisierung niemals zu weit von -1 schwankt.

So stellte Peierls fest, dass die Magnetisierung im Ising-Modell schließlich Superselektionssektoren definiert, getrennte Domänen, die nicht durch endliche Schwankungen verbunden sind.

Kramers-Wannier-Dualität[edit]

Kramers und Wannier konnten zeigen, dass die Hochtemperaturausdehnung und die Niedertemperaturausdehnung des Modells einer Gesamtskalierung der freien Energie gleichkommen. Dadurch konnte der Phasenübergangspunkt im zweidimensionalen Modell genau bestimmt werden (unter der Annahme, dass es einen eindeutigen kritischen Punkt gibt).

Yang-Lee-Nullen[edit]

Nach Onsagers Lösung untersuchten Yang und Lee, wie die Partitionsfunktion singulär wird, wenn sich die Temperatur der kritischen Temperatur nähert.

Monte-Carlo-Methoden zur numerischen Simulation[edit]

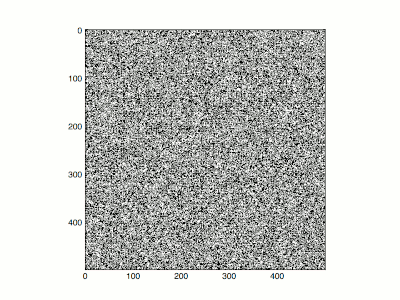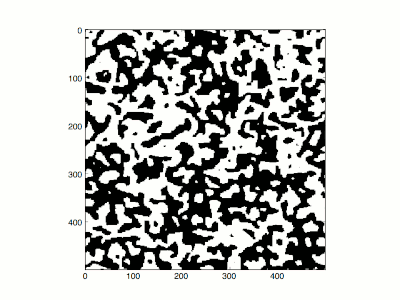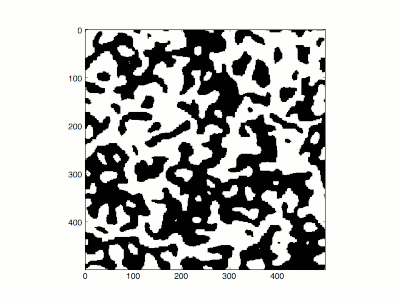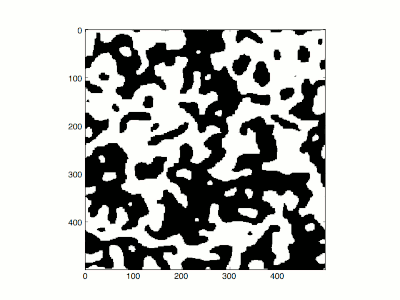
Abschrecken eines Ising-Systems auf einem zweidimensionalen quadratischen Gitter (500 × 500) mit inverser Temperatur β = 10, ausgehend von einer zufälligen Konfiguration

Definitionen[edit]

Das Ising-Modell kann oft schwierig numerisch zu bewerten sein, wenn das System viele Zustände enthält. Betrachten Sie ein Ising-Modell mit

L. = | Λ |: die Gesamtzahl der Stellen auf dem Gitter,

σ_j ∈ {−1, +1}: eine einzelne Spinstelle auf dem Gitter, j = 1, …, L.,

S. ∈ {−1, +1}^L.: Zustand des Systems.

Da jede Spinstelle ± 1 Spin hat, gibt es 2^L. verschiedene Zustände, die möglich sind.^[9] Dies motiviert den Grund für die Simulation des Ising-Modells mit Monte-Carlo-Methoden.^[9]

Der Hamilton-Operator, der üblicherweise zur Darstellung der Energie des Modells bei Verwendung von Monte-Carlo-Methoden verwendet wird, ist

${ displaystyle H ( sigma) = – J sum _ { langle i ~ j rangle} sigma _ {i} sigma _ {j} -h sum _ {j} sigma _ {j}. }}$

Darüber hinaus wird der Hamilton-Operator weiter vereinfacht, indem ein externes Feld von Null angenommen wird h, da viele Fragen, die mit dem Modell gelöst werden sollen, ohne externes Feld beantwortet werden können. Dies führt uns zu der folgenden Energiegleichung für den Zustand σ:

${ displaystyle H ( sigma) = – J sum _ { langle i ~ j rangle} sigma _ {i} sigma _ {j}.}$

Mit diesem Hamilton-Operator können interessierende Größen wie die spezifische Wärme oder die Magnetisierung des Magneten bei einer bestimmten Temperatur berechnet werden.^[9]

Metropolis-Algorithmus[edit]

Überblick[edit]

Der Metropolis-Hastings-Algorithmus ist der am häufigsten verwendete Monte-Carlo-Algorithmus zur Berechnung von Ising-Modellschätzungen.^[9] Der Algorithmus wählt zuerst Auswahlwahrscheinlichkeiten G(μ, ν), die die Wahrscheinlichkeit darstellen, dass der Zustand ν vom Algorithmus aus allen Zuständen ausgewählt wird, vorausgesetzt, einer befindet sich im Zustand μ. Es werden dann Akzeptanzwahrscheinlichkeiten verwendet EIN(μ, ν), so dass die detaillierte Bilanz erfüllt ist. Wenn der neue Zustand ν akzeptiert wird, wechseln wir in diesen Zustand und wiederholen dies, indem wir einen neuen Zustand auswählen und entscheiden, ihn zu akzeptieren. Wenn ν nicht akzeptiert wird, bleiben wir in μ. Dieser Vorgang wird wiederholt, bis ein Stoppkriterium erfüllt ist, was für das Ising-Modell häufig der Fall ist, wenn das Gitter ferromagnetisch wird, was bedeutet, dass alle Stellen in die gleiche Richtung zeigen.^[9]

Bei der Implementierung des Algorithmus muss dies sichergestellt werden G(μ, ν) wird so gewählt, dass die Ergodizität erfüllt ist. Im thermischen Gleichgewicht schwankt die Energie eines Systems nur in einem kleinen Bereich.^[9] Dies ist die Motivation hinter dem Konzept von Single-Spin-Flip-Dynamik, was besagt, dass wir bei jedem Übergang nur eine der Spinstellen auf dem Gitter ändern werden.^[9] Darüber hinaus kann man durch Verwendung der Single-Spin-Flip-Dynamik von jedem Zustand in einen anderen Zustand gelangen, indem jeder Ort, der sich zwischen den beiden Zuständen unterscheidet, einzeln umgedreht wird.

Das maximale Ausmaß der Änderung zwischen der Energie des gegenwärtigen Zustands, H._μ und jede mögliche neue Staatsenergie H._ν (unter Verwendung der Single-Spin-Flip-Dynamik) ist 2J. zwischen dem Spin wählen wir “Flip” in den neuen Zustand und den Nachbarn dieses Spins zu ziehen.^[9] In einem 1D Ising-Modell, in dem jeder Standort zwei Nachbarn hat (links und rechts), beträgt der maximale Energiedifferenz 4J..

Lassen c repräsentieren die Gitterkoordinationsnummer;; die Anzahl der nächsten Nachbarn, die ein Gitterplatz hat. Wir gehen davon aus, dass alle Standorte aufgrund periodischer Randbedingungen die gleiche Anzahl von Nachbarn haben.^[9] Es ist wichtig zu beachten, dass der Metropolis-Hastings-Algorithmus aufgrund der kritischen Verlangsamung um den kritischen Punkt herum nicht gut funktioniert. Andere Techniken wie Multigrid-Methoden, der Niedermayer-Algorithmus, der Swendsen-Wang-Algorithmus oder der Wolff-Algorithmus sind erforderlich, um das Modell in der Nähe des kritischen Punkts aufzulösen. eine Anforderung zur Bestimmung der kritischen Exponenten des Systems.

Spezifikation[edit]

Speziell für das Ising-Modell und unter Verwendung der Single-Spin-Flip-Dynamik kann Folgendes festgestellt werden.

Weil dort sind L. Gesamtzahl der Stellen auf dem Gitter, wobei Single-Spin-Flip der einzige Weg ist, um in einen anderen Zustand überzugehen, können wir sehen, dass es insgesamt gibt L. neue Zustände ν aus unserem gegenwärtigen Zustand μ. Der Algorithmus geht davon aus, dass die Auswahlwahrscheinlichkeiten gleich sind L. Zustände: G(μ, ν) = 1 /L.. Eine detaillierte Bilanz sagt uns, dass die folgende Gleichung gelten muss:

${ displaystyle { frac {P ( mu, nu)} {P ( nu, mu)}} = { frac {g ( mu, nu) A ( mu, nu)} { g ( nu, mu) A ( nu, mu)}} = { frac {A ( mu, nu)} {A ( nu, mu)}} = { frac {P_ { beta} ( nu)} {P _ { beta} ( mu)}} = { frac {{ frac {1} {Z}} e ^ {- beta (H _ { nu})}} {{ frac {1} {Z}} e ^ {- beta (H _ { mu})}} = e ^ {- beta (H _ { nu} -H _ { mu})}.}$

Daher möchten wir die Akzeptanzwahrscheinlichkeit auswählen, die unser Algorithmus erfüllen soll

${ displaystyle { frac {A ( mu, nu)} {A ( nu, mu)}} = e ^ {- beta (H _ { nu} -H _ { mu})}.}$

Wenn H._ν > H._μ, dann EIN(ν, μ)> EIN(μ, ν). Metropolis setzt das größere von EIN(μ, ν) oder EIN(ν, μ) ist 1. Nach dieser Überlegung lautet der Akzeptanzalgorithmus:^[9]

${ displaystyle A ( mu, nu) = { begin {case} e ^ {- beta (H _ { nu} -H _ { mu})}, & { text {if}} H _ { nu} -H _ { mu}> 0, \ 1 & { text {sonst}}. end {Fälle}}}$

${ displaystyle e ^ {- beta (H _ { nu} -H _ { mu})}.}$

Wiederholen.

Die Veränderung der Energie H._ν – – H._μ hängt nur vom Wert des Spins und seinen nächsten Graphnachbarn ab. Wenn der Graph also nicht zu verbunden ist, ist der Algorithmus schnell. Dieser Prozess erzeugt schließlich eine Auswahl aus der Verteilung.

Anzeigen des Ising-Modells als Markov-Kette[edit]

Es ist möglich, das Ising-Modell als Markov-Kette als unmittelbare Wahrscheinlichkeit anzusehen P._β(ν) des Übergangs in einen zukünftigen Zustand ν hängt nur vom gegenwärtigen Zustand μ ab. Der Metropolis-Algorithmus ist eigentlich eine Version einer Markov-Ketten-Monte-Carlo-Simulation, und da wir im Metropolis-Algorithmus die Single-Spin-Flip-Dynamik verwenden, kann jeder Zustand als mit genau verknüpft angesehen werden L. andere Zustände, in denen jeder Übergang dem Umdrehen einer einzelnen Spinstelle auf den entgegengesetzten Wert entspricht.^[10] Weiterhin ist da die Energiegleichung H._σ Die Änderung hängt nur von der Interaktionsstärke des nächsten Nachbarn ab J.Das Ising-Modell und seine Varianten wie das Sznajd-Modell können als eine Form eines Wählermodells für die Meinungsdynamik angesehen werden.

Eine Dimension[edit]

Die thermodynamische Grenze besteht, solange der Wechselwirkungsabfall vorliegt

${ displaystyle J_ {ij} sim | ij | ^ {- alpha}}$

mit α> 1.^[11]

• Im Falle von ferromagnetisch Interaktion
  ${ displaystyle J_ {ij} sim | ij | ^ {- alpha}}$

  mit 1 <α <2 hat Dyson im Vergleich zum hierarchischen Fall bewiesen, dass es einen Phasenübergang bei ausreichend kleiner Temperatur gibt.^[12]

• Im Falle von ferromagnetisch Interaktion
  ${ displaystyle J_ {ij} sim | ij | ^ {- 2}}$

  , Fröhlich und Spencer haben bewiesen, dass es einen Phasenübergang bei ausreichend kleiner Temperatur gibt (im Gegensatz zum hierarchischen Fall).^[13]

• Im Falle einer Interaktion
  ${ displaystyle J_ {ij} sim | ij | ^ {- alpha}}$

  mit α> 2 (was den Fall von Wechselwirkungen im endlichen Bereich einschließt) gibt es bei keiner positiven Temperatur (dh endlichem β) einen Phasenübergang, da die freie Energie in den thermodynamischen Parametern analytisch ist.^[11]

• Im Falle von unmittelbarer Nachbar Wechselwirkungen lieferte E. Ising eine genaue Lösung des Modells. Bei jeder positiven Temperatur (dh endlichem β) ist die freie Energie in den thermodynamischen Parametern analytisch, und die verkürzte Zweipunkt-Spin-Korrelation nimmt exponentiell schnell ab. Bei einer Temperatur von Null (dh unendlich β) gibt es einen Phasenübergang zweiter Ordnung: Die freie Energie ist unendlich und die verkürzte Zweipunkt-Spin-Korrelation nimmt nicht ab (bleibt konstant). Deshalb, T. = 0 ist die kritische Temperatur in diesem Fall. Skalierungsformeln sind erfüllt.^[14]

Isings genaue Lösung[edit]

Im Fall des nächsten Nachbarn (mit periodischen oder freien Randbedingungen) steht eine genaue Lösung zur Verfügung. Der Hamilton-Operator des eindimensionalen Ising-Modells auf einem Gitter von L. Standorte mit periodischen Randbedingungen ist

${ displaystyle H ( sigma) = – J sum _ {i = 1, ldots, L-1} sigma _ {i} sigma _ {i + 1} -h sum _ {i} sigma _{ich},}$

wo J. und h kann eine beliebige Zahl sein, da in diesem vereinfachten Fall J. ist eine Konstante, die die Wechselwirkungsstärke zwischen den nächsten Nachbarn und darstellt h ist das konstante externe Magnetfeld, das an Gitterstellen angelegt wird. Dann ist die freie Energie

${ displaystyle f ( beta, h) = – lim _ {L to infty} { frac {1} { beta L}} ln Z ( beta) = – { frac {1} { beta}} ln left (e ^ { beta J} cosh beta h + { sqrt {e ^ {2 beta J} ( sinh beta h) ^ {2} + e ^ {- 2 beta J}}} right),}$

und die Spin-Spin-Korrelation (dh die Kovarianz) ist

${ displaystyle langle sigma _ {i} sigma _ {j} rangle – langle sigma _ {i} rangle langle sigma _ {j} rangle = C ( beta) e ^ {- c ( beta) | ij |},}$

wo C.(β) und c(β) sind positive Funktionen für T. > 0. Für T. → 0 jedoch die inverse Korrelationslänge c(β) verschwindet.

Beweis[edit]

Der Beweis für dieses Ergebnis ist eine einfache Berechnung.

Wenn h = 0 ist es sehr einfach, die freie Energie im Fall einer freien Randbedingung zu erhalten, dh wenn

${ displaystyle H ( sigma) = – J ( sigma _ {1} sigma _ {2} + cdots + sigma _ {L-1} sigma _ {L}).}$

Dann faktorisiert das Modell unter Änderung der Variablen

${ displaystyle sigma ‘_ {j} = sigma _ {j} sigma _ {j-1}, quad j geq 2.}$

Das gibt

${ displaystyle Z ( beta) = sum _ { sigma _ {1}, ldots, sigma _ {L}} e ^ { beta J sigma _ {1} sigma _ {2}} e ^ { beta J sigma _ {2} sigma _ {3}} cdots e ^ { beta J sigma _ {L-1} sigma _ {L}} = 2 prod _ {j = 2 } ^ {L} sum _ { sigma ‘_ {j}} e ^ { beta J sigma’ _ {j}} = 2 left[e^{beta J}+e^{-beta J}right]^ {L-1}.}$

Daher ist die freie Energie

${ displaystyle f ( beta, 0) = – { frac {1} { beta}} ln left[e^{beta J}+e^{-beta J}right].}$

Mit der gleichen Änderung der Variablen

${ displaystyle langle sigma _ {j} sigma _ {j + N} rangle = left[{frac {e^{beta J}-e^{-beta J}}{e^{beta J}+e^{-beta J}}}right]^ {N},}$

daher zerfällt es exponentiell sobald T. ≠ 0; aber für T. = 0, dh in der Grenze β → ∞ gibt es keinen Zerfall.

Wenn h ≠ 0 Wir brauchen die Transfermatrix-Methode. Für die periodischen Randbedingungen ist der Fall der folgende. Die Partitionsfunktion ist

${ displaystyle Z ( beta) = sum _ { sigma _ {1}, ldots, sigma _ {L}} e ^ { beta h sigma _ {1}} e ^ { beta J Sigma _ {1} Sigma _ {2}} e ^ { beta h sigma _ {2}} e ^ { beta J sigma _ {2} sigma _ {3}} cdots e ^ { beta h sigma _ {L}} e ^ { beta J sigma _ {L} sigma _ {1}} = sum _ { sigma _ {1}, ldots, sigma _ {L}} V _ { sigma _ {1}, sigma _ {2}} V _ { sigma _ {2}, sigma _ {3}} cdots V _ { sigma _ {L}, sigma _ {1}} .}$

Die Koeffizienten

${ displaystyle V _ { sigma, sigma ‘}}$

kann als Einträge einer Matrix angesehen werden. Es gibt verschiedene Möglichkeiten: Eine bequeme (weil die Matrix symmetrisch ist) ist

${ displaystyle V _ { sigma, sigma ‘} = e ^ {{ frac { beta h} {2}} sigma} e ^ { beta J sigma sigma’} e ^ {{ frac { beta h} {2}} sigma ‘}}$

oder

${ displaystyle V = { begin {bmatrix} e ^ { beta (h + J)} & e ^ {- beta J} \ e ^ {- beta J} & e ^ {- beta (hJ)} end {bmatrix}}.}$

Im Matrixformalismus

${ displaystyle Z ( beta) = operatorname {Tr} left (V ^ {L} right) = lambda _ {1} ^ {L} + lambda _ {2} ^ {L} = lambda _ {1} ^ {L} left[1+left({frac {lambda _{2}}{lambda _{1}}}right)^{L}right],}$

wo λ₁ ist der höchste Eigenwert von V.während λ₂ ist der andere Eigenwert:

${ displaystyle lambda _ {1} = e ^ { beta J} cosh beta h + { sqrt {e ^ {2 beta J} ( sinh beta h) ^ {2} + e ^ {- 2 beta J}}},}$

und | λ₂| <λ₁. Dies ergibt die Formel der freien Energie.

[edit]

Die Energie des niedrigsten Zustands ist –J L, wenn alle Drehungen gleich sind. Bei jeder anderen Konfiguration beträgt die zusätzliche Energie 2J. mal die Anzahl der Vorzeichenänderungen, die beim Scannen der Konfiguration von links nach rechts auftreten.

Wenn wir die Anzahl der Vorzeichenwechsel in einer Konfiguration als festlegen kbeträgt der Energieunterschied zum niedrigsten Energiezustand 2k. Da die Energie in der Anzahl der Flips additiv ist, ist die Wahrscheinlichkeit p einen Spin-Flip an jeder Position zu haben, ist unabhängig. Das Verhältnis der Wahrscheinlichkeit, einen Flip zu finden, zur Wahrscheinlichkeit, einen nicht zu finden, ist der Boltzmann-Faktor:

${ displaystyle { frac {p} {1-p}} = e ^ {- 2 beta J}.}$

Das Problem reduziert sich auf unabhängige voreingenommene Münzwürfe. Dies vervollständigt im Wesentlichen die mathematische Beschreibung.

Aus der Beschreibung in Bezug auf unabhängige Würfe kann die Statistik des Modells für lange Schlangen verstanden werden. Die Zeile wird in Domänen aufgeteilt. Jede Domäne hat eine durchschnittliche Länge exp (2β). Die Länge einer Domäne ist exponentiell verteilt, da bei jedem Schritt, bei dem ein Flip auftritt, eine konstante Wahrscheinlichkeit besteht. Die Domänen werden niemals unendlich, so dass ein langes System niemals magnetisiert wird. Jeder Schritt reduziert die Korrelation zwischen einem Spin und seinem Nachbarn um einen Betrag proportional zu p, so fallen die Korrelationen exponentiell ab.

${ displaystyle langle S_ {i} S_ {j} rangle propto e ^ {- p | ij |}.}$

Die Partitionsfunktion ist das Volumen der Konfigurationen, wobei jede Konfiguration mit ihrem Boltzmann-Gewicht gewichtet wird. Da jede Konfiguration durch die Vorzeichenänderungen beschrieben wird, faktorisiert die Partitionsfunktion:

${ displaystyle Z = sum _ { text {configs}} e ^ { sum _ {k} S_ {k}} = prod _ {k} (1 + p) = (1 + p) ^ {L. }.}$

Der Logarithmus geteilt durch L. ist die freie Energiedichte:

${ displaystyle beta f = log (1 + p) = log left (1 + { frac {e ^ {- 2 beta J}} {1 + e ^ {- 2 beta J}}} Recht),}$

das ist analytisch weg von β = ∞. Ein Zeichen für einen Phasenübergang ist eine nicht analytische freie Energie, sodass das eindimensionale Modell keinen Phasenübergang aufweist.

Eindimensionale Lösung mit Querfeld[edit]

Um den Ising-Hamilton-Operator anhand einer quantenmechanischen Beschreibung von Spins auszudrücken, ersetzen wir die Spinvariablen durch ihre jeweiligen Pauli-Matrizen. Abhängig von der Richtung des Magnetfelds können wir jedoch einen Hamilton- oder Längsfeld-Hamilton-Operator erzeugen. Der Querfeld-Hamilton-Operator ist gegeben durch

${ displaystyle H ( sigma) = – J sum _ {i = 1, ldots, L} sigma _ {i} ^ {z} sigma _ {i + 1} ^ {z} -h sum _ {i} sigma _ {i} ^ {x}.}$

Das Transversalfeldmodell erfährt einen Phasenübergang zwischen einem geordneten und einem ungeordneten Regime bei J. ~ h. Dies kann durch eine Abbildung von Pauli-Matrizen gezeigt werden

${ displaystyle sigma _ {n} ^ {z} = prod _ {i = 1} ^ {n} T_ {i} ^ {x},}$

${ displaystyle sigma _ {n} ^ {x} = T_ {n} ^ {z} T_ {n + 1} ^ {z}.}$

Beim Umschreiben des Hamilton-Operators in Bezug auf diese Basisänderungsmatrizen erhalten wir

${ displaystyle H ( sigma) = – h sum _ {i = 1, ldots, L} T_ {i} ^ {z} T_ {i + 1} ^ {z} -J sum _ {i} T_ {i} ^ {x}.}$

Da die Rollen von h und J. geschaltet werden, macht der Hamiltonianer einen Übergang bei J. = h.^[15]

Zwei Dimensionen[edit]

• Im ferromagnetischen Fall gibt es einen Phasenübergang. Bei niedriger Temperatur beweist das Peierls-Argument eine positive Magnetisierung für den Fall des nächsten Nachbarn und dann durch die Griffiths-Ungleichung auch dann, wenn Wechselwirkungen mit größerer Reichweite hinzugefügt werden. Währenddessen liefert die Clusterexpansion bei hoher Temperatur eine Analyse der thermodynamischen Funktionen.
• Im Fall des nächsten Nachbarn wurde die freie Energie von Onsager durch die Äquivalenz des Modells mit freien Fermionen auf dem Gitter genau berechnet. Die Spin-Spin-Korrelationsfunktionen wurden von McCoy und Wu berechnet.

Die genaue Lösung von Onsager[edit]

Onsager (1944) erhielt den folgenden analytischen Ausdruck für die freie Energie des Ising-Modells auf dem anisotropen quadratischen Gitter beim Magnetfeld

${ displaystyle h = 0}$

in der thermodynamischen Grenze als Funktion der Temperatur und der horizontalen und vertikalen Wechselwirkungsenergien

${ displaystyle J_ {1}}$

und

${ displaystyle J_ {2}}$

, beziehungsweise

${ displaystyle – beta f = ln 2 + { frac {1} {8 pi ^ {2}}} int _ {0} ^ {2 pi} d theta _ {1} int _ {0} ^ {2 pi} d theta _ {2} ln[cosh(2beta J_{1})cosh(2beta J_{2})-sinh(2beta J_{1})cos(theta _{1})-sinh(2beta J_{2})cos(theta _{2})].}$

Aus diesem Ausdruck für die freie Energie können alle thermodynamischen Funktionen des Modells unter Verwendung einer geeigneten Ableitung berechnet werden. Das 2D-Ising-Modell war das erste Modell, das einen kontinuierlichen Phasenübergang bei einer positiven Temperatur aufwies. Es tritt bei der Temperatur auf

${ displaystyle T_ {c}}$

das löst die Gleichung

${ displaystyle sinh left ({ frac {2J_ {1}} {kT_ {c}} rechts) sinh left ({ frac {2J_ {2}} {kT_ {c}}} right ) = 1.}$

Im isotropen Fall, wenn die horizontalen und vertikalen Wechselwirkungsenergien gleich sind

${ displaystyle J_ {1} = J_ {2} = J}$

die kritische Temperatur

${ displaystyle T_ {c}}$

tritt am folgenden Punkt auf

${ displaystyle T_ {c} = { frac {2J} {k ln (1 + { sqrt {2}})}}$

Wenn die Wechselwirkungsenergien

${ displaystyle J_ {1}}$

,

${ displaystyle J_ {2}}$

beide negativ sind, wird das Ising-Modell zu einem Antiferromagneten. Da das quadratische Gitter zweigeteilt ist, ist es bei dieser Änderung beim Magnetfeld unveränderlich

${ displaystyle h = 0}$

Daher sind die freie Energie und die kritische Temperatur für den antiferromagnetischen Fall gleich. Für das Dreieckgitter, das nicht zweigeteilt ist, verhalten sich das ferromagnetische und das antiferromagnetische Ising-Modell deutlich unterschiedlich.

Matrix übertragen[edit]

Beginnen Sie mit einer Analogie zur Quantenmechanik. Das Ising-Modell auf einem langen periodischen Gitter hat eine Partitionsfunktion

${ displaystyle sum _ { {S }} exp { biggl (} sum _ {ij} S_ {i, j} left (S_ {i, j + 1} + S_ {i + 1, j} right) { biggr)}.}$

Denken Sie an die ich Richtung als Raum, und die j Richtung als Zeit. Dies ist eine unabhängige Summe aller Werte, die die Drehungen zu jedem Zeitpunkt annehmen können. Dies ist eine Art Pfadintegral, es ist die Summe aller Spin-Historien.

Ein Pfadintegral kann als Hamiltonsche Evolution umgeschrieben werden. Der Hamilton-Operator geht durch die Zeit, indem er eine einheitliche Rotation zwischen den Zeiten durchführt t und Zeit t + Δt::

${ displaystyle U = e ^ {iH Delta t}}$

Das Produkt der U-Matrizen nacheinander ist der Gesamtzeitentwicklungsoperator, der das Pfadintegral ist, mit dem wir begonnen haben.

${ displaystyle U ^ {N} = (e ^ {iH Delta t}) ^ {N} = int DXe ^ {iL}}$

wo N. ist die Anzahl der Zeitscheiben. Die Summe über alle Pfade ergibt sich aus einem Produkt von Matrizen, wobei jedes Matrixelement die Übergangswahrscheinlichkeit von einer Schicht zur nächsten ist.

In ähnlicher Weise kann man die Summe über alle Partitionsfunktionskonfigurationen in Schichten aufteilen, wobei jede Schicht zum Zeitpunkt 1 die eindimensionale Konfiguration ist. Dies definiert die Übertragungsmatrix:

${ displaystyle T_ {C_ {1} C_ {2}}.}$

Die Konfiguration in jedem Slice ist eine eindimensionale Sammlung von Spins. Zu jeder Zeitscheibe, T. hat Matrixelemente zwischen zwei Konfigurationen von Spins, eines in der unmittelbaren Zukunft und eines in der unmittelbaren Vergangenheit. Diese beiden Konfigurationen sind C.₁ und C.₂und sie sind alle eindimensionale Spin-Konfigurationen. Wir können uns den Vektorraum vorstellen, der T. wirkt wie alle komplexen linearen Kombinationen davon. Mit quantenmechanischer Notation:

${ displaystyle | A rangle = sum _ {S} A (S) | S rangle}$

wo jeder Basisvektor

${ displaystyle | S rangle}$

ist eine Spin-Konfiguration eines eindimensionalen Ising-Modells.

Wie der Hamilton-Operator wirkt die Übertragungsmatrix auf alle linearen Zustandskombinationen. Die Partitionsfunktion ist eine Matrixfunktion von T, die durch die Summe aller Historien definiert wird, die nachher zur ursprünglichen Konfiguration zurückkehren N. Schritte:

${ displaystyle Z = mathrm {tr} (T ^ {N}).}$

Da dies eine Matrixgleichung ist, kann sie auf jeder Basis ausgewertet werden. Also, wenn wir die Matrix diagonalisieren können T., wir können finden Z..

T. in Bezug auf Pauli-Matrizen[edit]

Der Beitrag zur Partitionsfunktion für jedes vergangene / zukünftige Konfigurationspaar auf einem Slice ist die Summe zweier Terme. Es gibt die Anzahl der Spin-Flips im letzten Slice und die Anzahl der Spin-Flips zwischen dem vergangenen und dem zukünftigen Slice. Definieren Sie einen Operator für Konfigurationen, der den Spin an Position i umdreht:

${ displaystyle sigma _ {i} ^ {x}.}$

In der üblichen Ising-Basis erzeugt sie, wenn sie auf eine beliebige lineare Kombination vergangener Konfigurationen einwirkt, dieselbe lineare Kombination, wobei jedoch der Spin an Position i jedes Basisvektors umgedreht wird.

Definieren Sie einen zweiten Operator, der den Basisvektor mit +1 und -1 gemäß dem Spin an der Position multipliziert ich::

${ displaystyle sigma _ {i} ^ {z}.}$

T. kann in Bezug auf diese geschrieben werden:

${ displaystyle sum _ {i} A sigma _ {i} ^ {x} + B sigma _ {i} ^ {z} sigma _ {i + 1} ^ {z}}$

wo EIN und B. sind Konstanten, die bestimmt werden sollen, um die Partitionsfunktion zu reproduzieren. Die Interpretation ist, dass die statistische Konfiguration an diesem Slice sowohl nach der Anzahl der Spinflips in dem Slice als auch danach, ob der Spin an der Position ist oder nicht, dazu beiträgt ich hat umgedreht.

Spin-Flip-Erstellungs- und Vernichtungsoperatoren[edit]

Genau wie im eindimensionalen Fall werden wir die Aufmerksamkeit von den Drehungen auf die Drehpunkte lenken. Das σ^z Begriff in T. zählt die Anzahl der Spin-Flips, die wir in Bezug auf Spin-Flip-Erstellungs- und Vernichtungsoperatoren schreiben können:

${ displaystyle sum C psi _ {i} ^ { dagger} psi _ {i}. ,}$

Der erste Term dreht einen Spin um, also je nach Basiszustand entweder:

1. Bewegt einen Spin-Flip um eine Einheit nach rechts
2. bewegt einen Spin-Flip eine Einheit nach links
3. erzeugt zwei Spin-Flips an benachbarten Standorten
4. zerstört zwei Spin-Flips an benachbarten Standorten.

Schreiben Sie dies in Form von Erstellungs- und Vernichtungsoperatoren auf:

${ displaystyle sigma _ {i} ^ {x} = D { psi ^ { dagger}} _ {i} psi _ {i + 1} + D ^ {*} { psi ^ { dagger} } _ {i} psi _ {i-1} + C psi _ {i} psi _ {i + 1} + C ^ {*} { psi ^ { Dolch}} _ {i} { psi ^ { dagger}} _ {i + 1}.}$

Ignorieren Sie die konstanten Koeffizienten und konzentrieren Sie sich auf das Formular. Sie sind alle quadratisch. Da die Koeffizienten konstant sind, bedeutet dies, dass die T. Die Matrix kann durch Fourier-Transformationen diagonalisiert werden.

Durch die Diagonalisierung wird die freie Energie des Onsager erzeugt.

Onsagers Formel für die spontane Magnetisierung[edit]

Onsager kündigte bekanntlich den folgenden Ausdruck für die spontane Magnetisierung an M. eines zweidimensionalen Ising-Ferromagneten auf dem quadratischen Gitter auf zwei verschiedenen Konferenzen im Jahr 1948, allerdings ohne Beweis^[8]

${ displaystyle M = left (1- left[sinh 2beta J_{1}sinh 2beta J_{2}right]^ {- 2} right) ^ { frac {1} {8}}}$

wo

${ displaystyle J_ {1}}$

und

${ displaystyle J_ {2}}$

sind horizontale und vertikale Wechselwirkungsenergien.

Eine vollständige Ableitung wurde erst 1951 von Yang (1952) unter Verwendung eines begrenzenden Prozesses von Transfermatrix-Eigenwerten gegeben. Der Beweis wurde später 1963 von Montroll, Potts und Ward stark vereinfacht^[8] unter Verwendung der Szegő-Grenzformel für Toeplitz-Determinanten durch Behandeln der Magnetisierung als Grenze der Korrelationsfunktionen.

Minimales Modell[edit]

Am kritischen Punkt ist das zweidimensionale Ising-Modell eine zweidimensionale konforme Feldtheorie. Die Spin- und Energiekorrelationsfunktionen werden durch ein Minimalmodell beschrieben, das genau gelöst wurde.

Drei Dimensionen[edit]

In drei wie in zwei Dimensionen ist der am besten untersuchte Fall des Ising-Modells das translatorisch invariante Modell auf einem kubischen Gitter mit Kopplung zum nächsten Nachbarn im Null-Magnetfeld. Top-Theoretiker suchten jahrzehntelang nach einer analytischen dreidimensionalen Lösung, die der Lösung von Onsager im zweidimensionalen Fall analog wäre.^[16] Inzwischen wird angenommen, dass es eine solche Lösung nicht gibt, obwohl es keinen Beweis gibt.

In drei Dimensionen wurde von Alexander Polyakov und Vladimir Dotsenko gezeigt, dass das Ising-Modell eine Darstellung in nicht wechselwirkenden fermionischen Strings aufweist. Diese Konstruktion wurde auf dem Gitter ausgeführt, und die Kontinuumsgrenze, die mutmaßlich den kritischen Punkt beschreibt, ist unbekannt.

Istrails NP-Vollständigkeitsergebnis für das allgemeine Spin-Glass-Modell[edit]

Im Jahr 2000 hat Sorin Istrail von Sandia National Laboratories bewiesen, dass das nichtplanare Ising-Modell NP-vollständig ist.^[17] Das heißt, vorausgesetzt P. ≠ NP, Das allgemeine Spin-Glass-Ising-Modell ist nur in planaren Fällen genau lösbar, sodass Lösungen für Abmessungen über zwei ebenfalls nicht lösbar sind. Das Ergebnis von Istrail betrifft nur das Spin-Glas-Modell mit räumlich variierenden Kopplungen und sagt nichts über Isings ursprüngliches ferromagnetisches Modell mit gleichen Kopplungen aus.

Phasenübergang[edit]

In drei wie in zwei Dimensionen zeigt Peierls Argument, dass es einen Phasenübergang gibt. Es ist bekannt, dass dieser Phasenübergang kontinuierlich ist (in dem Sinne, dass die Korrelationslänge divergiert und die Magnetisierung gegen Null geht) und als kritischer Punkt bezeichnet wird. Es wird angenommen, dass der kritische Punkt durch einen Fixpunkt der Renormierungsgruppe der Wilson-Kadanoff-Renormierungsgruppentransformation beschrieben werden kann. Es wird auch angenommen, dass der Phasenübergang durch eine dreidimensionale einheitliche konforme Feldtheorie beschrieben werden kann, wie durch Monte-Carlo-Simulationen belegt wird^[18][19] und theoretische Argumente.^[20] Obwohl es ein offenes Problem ist, das Bild der Renormierungsgruppe oder das Bild der konformen Feldtheorie genau zu bestimmen, haben theoretische Physiker diese beiden Methoden verwendet, um die kritischen Exponenten des Phasenübergangs zu berechnen, die mit den Experimenten und den Monte-Carlo-Simulationen übereinstimmen.

Diese konforme Feldtheorie, die den dreidimensionalen kritischen Ising-Punkt beschreibt, wird derzeit unter Verwendung der Methode des konformen Bootstraps untersucht.^{[21][22][23][24]} Diese Methode liefert derzeit die genauesten Informationen über die Struktur der kritischen Theorie (siehe Ising kritische Exponenten).

Vier Dimensionen und höher[edit]

In jeder Dimension kann das Ising-Modell durch ein lokal variierendes mittleres Feld produktiv beschrieben werden. Das Feld ist definiert als der durchschnittliche Spinwert über einen großen Bereich, jedoch nicht so groß, dass das gesamte System eingeschlossen ist. Das Feld variiert immer noch langsam von Punkt zu Punkt, wenn sich das Durchschnittsvolumen bewegt. Diese Feldschwankungen werden durch eine Kontinuumsfeldtheorie in der unendlichen Systemgrenze beschrieben.

Lokales Feld[edit]

Das Feld H. ist definiert als die langwelligen Fourier-Komponenten der Spinvariablen in der Grenze, in der die Wellenlängen lang sind. Es gibt viele Möglichkeiten, den langwelligen Durchschnitt zu ermitteln, abhängig von den Details, wie hohe Wellenlängen abgeschnitten werden. Die Details sind nicht zu wichtig, da das Ziel darin besteht, die Statistiken von zu finden H. und nicht die Drehungen. Sobald die Korrelationen in H. bekannt sind, sind die Fernkorrelationen zwischen den Spins proportional zu den Fernkorrelationen in H..

Für jeden Wert des sich langsam ändernden Feldes H.ist die freie Energie (log-Wahrscheinlichkeit) eine lokale analytische Funktion von H. und seine Gradienten. Die freie Energie F.((H.) ist definiert als die Summe aller Ising-Konfigurationen, die mit dem langwelligen Feld übereinstimmen. Schon seit H. ist eine grobe Beschreibung, es gibt viele Ising-Konfigurationen, die mit jedem Wert von übereinstimmen H., solange für das Match nicht zu viel Genauigkeit erforderlich ist.

Da der zulässige Wertebereich des Spins in jeder Region nur von den Werten von abhängt H. Innerhalb eines Mittelungsvolumens aus dieser Region hängt der Beitrag der freien Energie aus jeder Region nur vom Wert von ab H. dort und in den Nachbarregionen. Damit F. ist eine Summe über alle Regionen eines lokalen Beitrags, die nur davon abhängt H. und seine Derivate.

Durch Symmetrie in H., nur gerade Kräfte tragen dazu bei. Durch Reflexionssymmetrie auf einem quadratischen Gitter tragen nur gleichmäßige Potenzen von Gradienten bei. Schreiben Sie die ersten Begriffe in die freie Energie:

${ displaystyle beta F = int d ^ {d} x left[AH^{2}+sum _{i=1}^{d}Z_{i}(partial _{i}H)^{2}+lambda H^{4}+cdots right].}$

Auf einem quadratischen Gitter garantieren Symmetrien, dass die Koeffizienten Z._ich der abgeleiteten Terme sind alle gleich. Aber auch für ein anisotropes Ising-Modell, bei dem die Z._ich‘s in verschiedene Richtungen sind unterschiedlich, die Schwankungen in H. sind in einem Koordinatensystem isotrop, in dem die verschiedenen Raumrichtungen neu skaliert werden.

Auf jedem Gitter der abgeleitete Term

${ displaystyle Z_ {ij} , teilweise _ {i} H , teilweise _ {j} H}$

ist eine positive bestimmte quadratische Form und kann verwendet werden definieren die Metrik für den Raum. Jedes translatorisch invariante Ising-Modell ist also über große Entfernungen in koordinierten Koordinaten rotationsinvariant Z._ij = δ_ij. Rotationssymmetrie tritt in großen Entfernungen spontan auf, nur weil es nicht sehr viele Terme niedriger Ordnung gibt. An multikritischen Punkten höherer Ordnung geht diese zufällige Symmetrie verloren.

Da βF. ist eine Funktion eines sich langsam räumlich ändernden Feldes, die Wahrscheinlichkeit einer Feldkonfiguration ist:

${ displaystyle P (H) propto e ^ {- int d ^ {d} x left[AH^{2}+Z|nabla H|^{2}+lambda H^{4}right]}.}$

Der statistische Durchschnitt eines Produkts von H. Begriffe ist gleich:

${ displaystyle langle H (x_ {1}) H (x_ {2}) cdots H (x_ {n}) rangle = { int DH , P (H) H (x_ {1}) H ( x_ {2}) cdots H (x_ {n}) über int DH , P (H)}.}$

Der Nenner in diesem Ausdruck heißt Partitionsfunktionund das Integral über alle möglichen Werte von H. ist ein statistisches Pfadintegral. Es integriert exp (βF.) über alle Werte von H.über alle langwelligen Fourier-Komponenten der Spins. F. ist ein euklidischer Lagrange für das Feld H.Der einzige Unterschied zwischen dieser und der Quantenfeldtheorie eines Skalarfeldes besteht darin, dass alle abgeleiteten Terme mit einem positiven Vorzeichen eintreten und es keinen Gesamtfaktor von gibt ich.

${ displaystyle Z = int DH , e ^ {- int d ^ {d} x left[AH^{2}+Z|nabla H|^{2}+lambda H^{4}right]}}$

Dimensionsanalyse[edit]

Die Form von F. kann verwendet werden, um vorherzusagen, welche Begriffe durch Dimensionsanalyse am wichtigsten sind. Die Dimensionsanalyse ist nicht ganz einfach, da die Skalierung von H. muss bestimmt werden.

Im allgemeinen Fall wählen Sie das Skalierungsgesetz für H. ist einfach, da der einzige Begriff, der dazu beiträgt, der erste ist,

${ displaystyle F = int d ^ {d} x , AH ^ {2}.}$

Dieser Begriff ist der bedeutendste, aber er gibt triviales Verhalten. Diese Form der freien Energie ist ultralokal, was bedeutet, dass es sich um eine Summe eines unabhängigen Beitrags von jedem Punkt handelt. Dies ist wie bei den Spin-Flips im eindimensionalen Ising-Modell. Jeder Wert von H. an jedem Punkt schwankt völlig unabhängig vom Wert an jedem anderen Punkt.

Die Skala des Feldes kann neu definiert werden, um den Koeffizienten zu absorbieren EINund dann ist es klar, dass EIN bestimmt nur das Gesamtmaß der Schwankungen. Das ultralokale Modell beschreibt das langwellige Hochtemperaturverhalten des Ising-Modells, da in dieser Grenze die Fluktuationsmittelwerte von Punkt zu Punkt unabhängig sind.

Um den kritischen Punkt zu finden, senken Sie die Temperatur. Wenn die Temperatur sinkt, schwanken die Schwankungen in H. steigen, weil die Schwankungen mehr korreliert sind. Dies bedeutet, dass der Durchschnitt einer großen Anzahl von Drehungen nicht so schnell klein wird, als ob sie nicht korreliert wären, da sie dazu neigen, gleich zu sein. Dies entspricht einer Abnahme EIN im Einheitensystem wo H. absorbiert nicht EIN. Der Phasenübergang kann nur erfolgen, wenn die untergeordneten Begriffe in F. kann dazu beitragen, aber da der erste Term auf große Entfernungen dominiert, ist der Koeffizient EIN muss auf Null eingestellt werden. Dies ist der Ort des kritischen Punktes:

${ displaystyle F = int d ^ {d} x left[tH^{2}+lambda H^{4}+Z(nabla H)^{2}right],}$

wo t ist ein Parameter, der beim Übergang durch Null geht.

Schon seit t verschwindet, wenn die Größe des Feldes mit diesem Begriff festgelegt wird, explodieren die anderen Begriffe. Einmal t klein ist, kann der Maßstab des Feldes entweder eingestellt werden, um den Koeffizienten von festzulegen H.⁴ Begriff oder die (∇H.)² Begriff zu 1.

Magnetisierung[edit]

Um die Magnetisierung zu finden, korrigieren Sie die Skalierung von H. so dass λ eins ist. Nun das Feld H. hat Dimension –d/ 4, damit H.⁴d^dx ist dimensionslos und Z. hat Dimension 2 – d/ 2. Bei dieser Skalierung ist der Gradiententerm nur bei großen Entfernungen für wichtig d ≤ 4. Oberhalb von vier Dimensionen wird bei langen Wellenlängen die Gesamtmagnetisierung nur durch die ultralokalen Terme beeinflusst.

Es gibt einen subtilen Punkt. Das Feld H. schwankt statistisch und die Schwankungen können den Nullpunkt von verschieben t. Um zu sehen, wie, überlegen Sie H.⁴ auf folgende Weise aufteilen:

${ displaystyle H (x) ^ {4} = – langle H (x) ^ {2} rangle ^ {2} +2 langle H (x) ^ {2} rangle H (x) ^ {2 } + left (H (x) ^ {2} – langle H (x) ^ {2} rangle right) ^ {2}}$

Der erste Term ist ein konstanter Beitrag zur freien Energie und kann ignoriert werden. Der zweite Term ist eine endliche Verschiebung in t. Der dritte Term ist eine Größe, die auf große Entfernungen auf Null skaliert. Dies bedeutet, dass bei der Analyse der Skalierung von t durch dimensionale Analyse ist es die Verschiebung t das ist wichtig. Dies war historisch sehr verwirrend, weil die Verschiebung in t zu jedem endlichen λ ist endlich, aber in der Nähe des Übergangs t ist sehr klein. Die gebrochene Änderung in t ist sehr groß und in Einheiten, in denen t ist fest, die Verschiebung sieht unendlich aus.

Die Magnetisierung ist auf dem Minimum der freien Energie, und dies ist eine analytische Gleichung. In Bezug auf die verschoben t,

${ displaystyle { partiell über partiell H} links (tH ^ {2} + lambda H ^ {4} rechts) = 2tH + 4 lambda H ^ {3} = 0}$

Zum t <0 sind die Minima bei H. proportional zur Quadratwurzel von t. Landaus Katastrophenargument ist also in Dimensionen größer als 5 korrekt. Der Magnetisierungsexponent in Dimensionen größer als 5 ist gleich dem mittleren Feldwert.

Wann t negativ ist, werden die Schwankungen um das neue Minimum durch einen neuen positiven quadratischen Koeffizienten beschrieben. Da dieser Begriff immer dominiert, werden die Schwankungen bei Temperaturen unterhalb des Übergangs auf große Entfernungen wieder ultralokal.

Schwankungen[edit]

Um das Verhalten von Schwankungen zu ermitteln, skalieren Sie das Feld neu, um den Gradiententerm festzulegen. Dann beträgt die Längenskalierungsdimension des Feldes 1 – d/ 2. Jetzt hat das Feld bei allen Temperaturen konstante quadratische räumliche Schwankungen. Die Skalendimension des H.² Term ist 2, während die Skalendimension der H.⁴ Laufzeit ist 4 – d. Zum d <4, die H.⁴ Begriff hat positive Skalendimension. Bei Abmessungen über 4 hat es negative Skalenabmessungen.

Dies ist ein wesentlicher Unterschied. Bei Abmessungen über 4 bedeutet das Festlegen der Skala des Gradiententerms, dass der Koeffizient von H.⁴ Begriff ist bei immer längeren Wellenlängen immer weniger wichtig. Die Dimension, in der nichtquadratische Beiträge anfangen, Beiträge zu leisten, wird als kritische Dimension bezeichnet. Im Ising-Modell beträgt die kritische Dimension 4.

In Dimensionen über 4 werden die kritischen Schwankungen durch eine rein quadratische freie Energie bei langen Wellenlängen beschrieben. Dies bedeutet, dass die Korrelationsfunktionen alle als Gaußsche Mittelwerte berechnet werden können:

${ displaystyle langle S (x) S (y) rangle propto langle H (x) H (y) rangle = G (xy) = int {dk over (2 pi) ^ {d} } {e ^ {ik (xy)} over k ^ {2} + t}}$

gültig wann x – – y ist groß. Die Funktion G((x – – y) ist die analytische Fortsetzung der imaginären Zeit des Feynman-Propagators, da die freie Energie die analytische Fortsetzung der Quantenfeldwirkung für ein freies Skalarfeld ist. Für Dimensionen 5 und höher werden dann alle anderen Korrelationsfunktionen bei großen Entfernungen durch den Wickschen Satz bestimmt. Alle ungeraden Momente sind durch ± Symmetrie Null. Die geraden Momente sind die Summe aller Partitionen in Paare des Produkts von G((x – – y) für jedes Paar.

${ displaystyle langle S (x_ {1}) S (x_ {2}) cdots S (x_ {2n}) rangle = C ^ {n} sum G (x_ {i1}, x_ {j1}) G (x_ {i2}, x_ {j2}) ldots G (x_ {in}, x_ {jn})}$

wo C. ist die Proportionalitätskonstante. Also wissen G reicht. Es bestimmt alle Mehrpunktkorrelationen des Feldes.

Die kritische Zweipunktfunktion[edit]

Um die Form von zu bestimmen GBedenken Sie, dass die Felder in einem Pfadintegral den klassischen Bewegungsgleichungen entsprechen, die durch Variation der freien Energie abgeleitet werden:

${ displaystyle { begin {align} && left (- nabla _ {x} ^ {2} + t right) langle H (x) H (y) rangle & = 0 \ rightarrow {} && nabla ^ {2} G (x) + tG (x) & = 0 end {align}}}$

Dies gilt nur an nicht zufälligen Punkten, da die Korrelationen von H. sind singulär, wenn Punkte kollidieren. H. gehorcht klassischen Bewegungsgleichungen aus dem gleichen Grund, aus dem quantenmechanische Operatoren ihnen gehorchen – ihre Schwankungen werden durch ein Pfadintegral definiert.

Am kritischen Punkt t = 0, dies ist die Laplace-Gleichung, die nach der Gaußschen Methode aus der Elektrostatik gelöst werden kann. Definieren Sie ein elektrisches Feldanalog durch

${ displaystyle E = nabla G}$

Weg vom Ursprung:

${ displaystyle nabla cdot E = 0}$

schon seit G ist sphärisch symmetrisch in d Abmessungen und E. ist der radiale Gradient von G. Integration über eine große d – 1 dimensionale Kugel,

${ displaystyle int d ^ {d-1} SE_ {r} = mathrm {Konstante}}$

Das gibt:

${ displaystyle E = {C over r ^ {d-1}}}$

und G kann durch Integration in Bezug auf gefunden werden r.

${ displaystyle G (r) = {C over r ^ {d-2}}}$

Die Konstante C. behebt die allgemeine Normalisierung des Feldes.

G((r) vom kritischen Punkt entfernt[edit]

Wann t ist nicht gleich Null, so dass H. schwankt bei einer Temperatur, die etwas von der kritischen entfernt ist, zerfällt die Zweipunktfunktion auf große Entfernungen. Die Gleichung, der es folgt, wird geändert:

${ displaystyle nabla ^ {2} G + tG = 0 bis {1 über r ^ {d-1}} {d über dr} left (r ^ {d-1} {dG über dr} rechts) + tG (r) = 0}$

Zum r klein im Vergleich zu

${ displaystyle { sqrt {t}}}$

Die Lösung divergiert genauso wie im kritischen Fall, aber das Fernverhalten wird geändert.

Um zu sehen, wie es ist, ist es zweckmäßig, die von Schwinger im Kontext der Quantenfeldtheorie eingeführte Zweipunktfunktion als Integral darzustellen:

${ displaystyle G (x) = int d tau {1 over left ({ sqrt {2 pi tau}} right) ^ {d}} e ^ {- {x ^ {2} über 4 tau} -t tau}}$

Das ist G, da die Fourier-Transformation dieses Integrals einfach ist. Jeder feste τ-Beitrag ist ein Gaußscher Beitrag x, dessen Fourier-Transformation ein weiterer Gaußscher Wert der reziproken Breite in ist k.

${ displaystyle G (k) = int d tau e ^ {- (k ^ {2} -t) tau} = {1 über k ^ {2} -t}}$

Dies ist die Umkehrung des Operators ∇² – – t im k-space, wirkt auf die Einheitsfunktion in k-space, bei dem es sich um die Fourier-Transformation einer am Ursprung lokalisierten Delta-Funktionsquelle handelt. Es erfüllt also die gleiche Gleichung wie G mit den gleichen Randbedingungen, die die Stärke der Divergenz bei 0 bestimmen.

Die Interpretation der integralen Darstellung über die richtige Zeit τ ist, dass die Zweipunktfunktion die Summe über alle zufälligen Gehwege ist, die Position 0 mit Position verbinden x über die Zeit τ. Die Dichte dieser Pfade zum Zeitpunkt τ an der Position x ist Gaußsch, aber die zufälligen Wanderer verschwinden mit einer konstanten Rate proportional zu t so dass der Gaußsche zum Zeitpunkt τ in der Höhe um einen Faktor verringert wird, der stetig exponentiell abnimmt. Im Kontext der Quantenfeldtheorie sind dies die Pfade relativistisch lokalisierter Quanten in einem Formalismus, der den Pfaden einzelner Teilchen folgt. Im rein statistischen Kontext erscheinen diese Pfade immer noch durch die mathematische Entsprechung mit Quantenfeldern, aber ihre Interpretation ist weniger direkt physikalisch.

Die integrale Darstellung zeigt dies sofort G((r) ist positiv, da es als gewichtete Summe positiver Gaußscher dargestellt wird. Es gibt auch die Abklingrate bei großem r an, da die richtige Zeit für einen zufälligen Gang zum Erreichen der Position τ r ist² und in dieser Zeit ist die Gaußsche Höhe um abgenommen

${ displaystyle e ^ {- t tau} = e ^ {- tr ^ {2}}}$

. Der für die Position geeignete Abklingfaktor r ist deshalb

${ displaystyle e ^ {- { sqrt {t}} r}}$

.

Eine heuristische Annäherung für G((r) ist:

${ displaystyle G (r) approx {e ^ {- { sqrt {t}} r} over r ^ {d-2}}}$

Dies ist keine exakte Form, außer in drei Dimensionen, in denen Interaktionen zwischen Pfaden wichtig werden. Die genauen Formen in hohen Dimensionen sind Varianten von Bessel-Funktionen.

Symanzik Polymer Interpretation[edit]

Die Interpretation der Korrelationen als Quanten fester Größe, die sich entlang zufälliger Spaziergänge bewegen, gibt einen Weg zu verstehen, warum die kritische Dimension der H.⁴ Interaktion ist 4. Der Begriff H.⁴ kann als das Quadrat der Dichte der zufälligen Wanderer an jedem Punkt betrachtet werden. Damit ein solcher Term die Korrelationsfunktionen endlicher Ordnung ändert, die nur wenige neue zufällige Spaziergänge in die schwankende Umgebung einführen, müssen sich die neuen Pfade schneiden. Ansonsten ist das Quadrat der Dichte nur proportional zur Dichte und verschiebt nur die H.² Koeffizient durch eine Konstante. Die Schnittwahrscheinlichkeit von zufälligen Spaziergängen hängt jedoch von der Dimension ab, und zufällige Spaziergänge in Dimensionen über 4 schneiden sich nicht.

Die fraktale Dimension eines gewöhnlichen Zufallslaufs beträgt 2. Die Anzahl der Kugeln der Größe ε, die erforderlich sind, um den Pfad abzudecken, nimmt mit ε zu⁻². Zwei Objekte der fraktalen Dimension 2 schneiden sich mit angemessener Wahrscheinlichkeit nur in einem Raum der Dimension 4 oder weniger, die gleiche Bedingung wie für ein generisches Ebenenpaar. Kurt Symanzik argumentierte, dass dies impliziert, dass die kritischen Ising-Schwankungen in Dimensionen über 4 durch ein freies Feld beschrieben werden sollten. Dieses Argument wurde schließlich ein mathematischer Beweis.

4 – ε Dimensionen – Renormierungsgruppe[edit]

Das Ising-Modell in vier Dimensionen wird durch ein schwankendes Feld beschrieben, aber jetzt interagieren die Schwankungen. In der Polymerdarstellung sind Schnittpunkte von zufälligen Spaziergängen nur geringfügig möglich. In der Quantenfeldfortsetzung interagieren die Quanten.

Der negative Logarithmus der Wahrscheinlichkeit einer Feldkonfiguration H. ist die freie Energiefunktion

${ displaystyle F = int d ^ {4} x left[{Z over 2}|nabla H|^{2}+{t over 2}H^{2}+{lambda over 4!}H^{4}right],}$

Die numerischen Faktoren dienen dazu, die Bewegungsgleichungen zu vereinfachen. Ziel ist es, die statistischen Schwankungen zu verstehen. Wie jedes andere nicht quadratische Pfadintegral haben die Korrelationsfunktionen eine Feynman-Expansion als Partikel, die sich entlang zufälliger Spaziergänge bewegen, sich an Eckpunkten teilen und wieder verbinden. Die Wechselwirkungsstärke wird durch die klassisch dimensionslose Größe λ parametrisiert.

Obwohl die Dimensionsanalyse zeigt, dass sowohl λ als auch Z. sind dimensionslos, das ist irreführend. Die langwelligen statistischen Schwankungen sind nicht genau skalierungsinvariant und werden erst dann skalierungsinvariant, wenn die Wechselwirkungsstärke verschwindet.

Der Grund ist, dass es einen Cutoff gibt, der zum Definieren verwendet wird H.und der Cutoff definiert die kürzeste Wellenlänge. Schwankungen von H. bei Wellenlängen nahe dem Cutoff können die längerwelligen Schwankungen beeinflusst werden. Wenn das System zusammen mit dem Cutoff skaliert wird, werden die Parameter durch Dimensionsanalyse skaliert. Beim Vergleichen von Parametern wird das Verhalten jedoch nicht verglichen, da das neu skalierte System über mehr Modi verfügt. Wenn das System so neu skaliert wird, dass der kurzwellige Grenzwert fest bleibt, werden die langwelligen Schwankungen modifiziert.

Wilson-Renormierung[edit]

Eine schnelle heuristische Methode zum Studieren der Skalierung besteht darin, die Skalierung abzuschneiden H. Wellenzahlen an einem Punkt λ. Fourier-Modi von H. mit Wellenzahlen größer als λ dürfen nicht schwanken. Eine Neuskalierung der Länge, die das gesamte System kleiner macht, erhöht alle Wellenzahlen und verschiebt einige Schwankungen über den Grenzwert.

Um den alten Grenzwert wiederherzustellen, führen Sie eine teilweise Integration aller Wellenzahlen durch, die früher verboten waren, jetzt aber schwanken. In Feynman-Diagrammen Integration über einen schwankenden Modus bei Wellenzahl k verbindet Linien, die Schwung tragen k in einer Korrelationsfunktion paarweise mit einem Faktor des inversen Propagators.

Beim erneuten Skalieren, wenn das System um den Faktor (1+) verkleinert wirdb), das t Der Koeffizient erhöht sich um einen Faktor (1+)b)² durch dimensionale Analyse. Die Änderung in t für infinitesimal b ist 2bt. Die beiden anderen Koeffizienten sind dimensionslos und ändern sich überhaupt nicht.

Der Effekt der Integration niedrigster Ordnung kann aus den Bewegungsgleichungen berechnet werden:

${ displaystyle nabla ^ {2} H + tH = – { lambda over 6} H ^ {3}.}$

Diese Gleichung ist eine Identität innerhalb einer Korrelationsfunktion, die von anderen Einfügungen entfernt ist. Nach der Integration der Modi mit Λ k <(1+b) Λ wird es eine etwas andere Identität sein.

Da die Form der Gleichung erhalten bleibt, reicht es aus, die Änderung der Koeffizienten zu analysieren, um die Änderung der Koeffizienten zu ermitteln H.³ Begriff. In einer Feynman-Diagrammerweiterung wird die H.³ Term in einer Korrelationsfunktion innerhalb einer Korrelation hat drei baumelnde Linien. Verbinden Sie zwei von ihnen mit großer Wellenzahl k gibt eine Änderung H.³ mit einer baumelnden Linie, also proportional zu H.::

${ displaystyle delta H ^ {3} = 3H int _ { Lambda <| k | <(1 + b) Lambda} {d ^ {4} k over (2 pi) ^ {4}} {1 over (k ^ {2} + t)}}$

Der Faktor 3 ergibt sich aus der Tatsache, dass die Schleife auf drei verschiedene Arten geschlossen werden kann.

Das Integral sollte in zwei Teile geteilt werden:

${ displaystyle int dk {1 über k ^ {2}} – t int dk {1 über k ^ {2} (k ^ {2} + t)} = A Lambda ^ {2} b + Bbt}$

Der erste Teil ist nicht proportional zu tund in der Bewegungsgleichung kann es durch eine konstante Verschiebung in absorbiert werden t. Es wird durch die Tatsache verursacht, dass die H.³ Term hat einen linearen Teil. Nur der zweite Begriff, der von abweicht t zu tträgt zur kritischen Skalierung bei.

Dieser neue lineare Term ergänzt den ersten Term auf der linken Seite und ändert sich t um einen Betrag proportional zu t. Die Gesamtänderung in t ist die Summe des Begriffs aus der Dimensionsanalyse und dieses zweiten Begriffs aus Bedienerprodukten:

${ displaystyle delta t = left (2- {B lambda over 2} right) bt}$

Damit t wird neu skaliert, aber seine Dimension ist anomal, es wird um einen Betrag geändert, der proportional zum Wert von λ ist.

Aber auch λ ändert sich. Die Änderung von λ erfordert die Berücksichtigung der Teilung der Linien und der schnellen Wiederverbindung. Der Prozess niedrigster Ordnung ist einer, aus dem eine der drei Zeilen stammt H.³ teilt sich in drei Teile, die sich schnell mit einer der anderen Linien desselben Scheitelpunkts verbinden. Die Korrektur zum Scheitelpunkt ist

${ displaystyle delta lambda = – {3 lambda ^ {2} over 2} int _ {k} dk {1 over (k ^ {2} + t) ^ {2}} = – {3 lambda ^ {2} over 2} b}$

Der numerische Faktor ist dreimal größer, da bei der Auswahl der drei neuen Linien, die kontrahiert werden sollen, ein zusätzlicher Faktor von drei hinzukommt. Damit

${ displaystyle delta lambda = -3B lambda ^ {2} b}$

Diese beiden Gleichungen definieren zusammen die Renormierungsgruppengleichungen in vier Dimensionen:

${ displaystyle { begin {align} {dt over t} & = left (2- {B lambda over 2} right) b \ {d lambda over lambda} & = {- 3B lambda over 2} b end {align}}}$

Der Koeffizient B. wird durch die Formel bestimmt

${ displaystyle Bb = int _ { Lambda <| k | <(1 + b) Lambda} {d ^ {4} k over (2 pi) ^ {4}} {1 over k ^ { 4}}}$

und ist proportional zur Fläche einer dreidimensionalen Kugel mit dem Radius λ multipliziert mit der Breite des Integrationsbereichs bΛ geteilt durch Λ⁴::

${ displaystyle B = (2 pi ^ {2} Lambda ^ {3}) {1 over (2 pi) ^ {4}} {b Lambda} {1 over b Lambda ^ {4} } = {1 over 8 pi ^ {2}}}$

In anderen Dimensionen ist die Konstante B. ändert sich, aber die gleiche Konstante erscheint beide in der t Strömung und in der Kupplungsströmung. Der Grund ist, dass die Ableitung in Bezug auf t der geschlossenen Schleife mit einem einzelnen Scheitelpunkt ist eine geschlossene Schleife mit zwei Scheitelpunkten. Dies bedeutet, dass der einzige Unterschied zwischen der Skalierung der Kopplung und der t ist der kombinatorische Faktor beim Verbinden und Teilen.

Wilson-Fisher-Fixpunkt[edit]

Die Untersuchung von drei Dimensionen ausgehend von der vierdimensionalen Theorie sollte möglich sein, da die Schnittwahrscheinlichkeiten zufälliger Spaziergänge kontinuierlich von der Dimensionalität des Raums abhängen. In der Sprache der Feynman-Graphen ändert sich die Kopplung nicht sehr, wenn die Dimension geändert wird.

Der Prozess, von Dimension 4 fortzufahren, ist ohne ein Rezept dafür nicht genau definiert. Das Rezept ist nur in Diagrammen gut definiert. Es ersetzt die Schwinger-Darstellung in Dimension 4 durch die Schwinger-Darstellung in Dimension 4 – ε definiert durch:

${ displaystyle G (xy) = int d tau {1 über t ^ {d über 2}} e ^ {{x ^ {2} über 2 tau} + t tau}}$

In Dimension 4 – & egr; hat die Kopplung & lgr; eine positive Skalendimension & egr;, und diese muss zur Strömung hinzugefügt werden.

${ displaystyle { begin {align} {d lambda over lambda} & = varepsilon -3B lambda \ {dt over t} & = 2- lambda B end {align}}}$

Der Koeffizient B. ist dimensionsabhängig, wird jedoch abgebrochen. Der Fixpunkt für λ ist nicht mehr Null, sondern bei:

${ displaystyle lambda = { varepsilon over 3B}}$

wo die Skalenabmessungen von t wird um einen Betrag λ verändertB. = ε / 3.

Der Magnetisierungsexponent wird proportional geändert zu:

${ displaystyle { tfrac {1} {2}} left (1 – { varepsilon over 3} right)}$

Dies ist 0,333 in 3 Dimensionen (& epsi; = 1) und 0,166 in 2 Dimensionen (& epsi; = 2). Dies ist nicht so weit vom gemessenen Exponenten .308 und dem zweidimensionalen Onsager-Exponenten .125 entfernt.

Unendliche Dimensionen – mittleres Feld[edit]

Das Verhalten eines Ising-Modells in einem vollständig verbundenen Graphen kann durch die mittlere Feldtheorie vollständig verstanden werden. Diese Art der Beschreibung eignet sich für sehr hochdimensionale quadratische Gitter, da dann jeder Standort eine sehr große Anzahl von Nachbarn hat.

Die Idee ist, dass, wenn jeder Spin mit einer großen Anzahl von Spins verbunden ist, nur das durchschnittliche Verhältnis von + Spins zu – Spins wichtig ist, da die Schwankungen um diesen Mittelwert gering sind. Das mittlere Feld H. ist der durchschnittliche Anteil der Spins, die + minus dem durchschnittlichen Anteil der Spins sind, die – sind. Die Energiekosten für das Umdrehen eines einzelnen Spins im mittleren Feld H. ist ± 2JNH. Es ist bequem neu zu definieren J. den Faktor zu absorbieren N., so dass die Grenze N. → ∞ ist glatt. In Bezug auf das Neue J.betragen die Energiekosten für das Umdrehen eines Spins ± 2JH.

Diese Energiekosten geben das Wahrscheinlichkeitsverhältnis an p dass der Spin + zur Wahrscheinlichkeit 1− istp dass der Spin ist -. Dieses Verhältnis ist der Boltzmann-Faktor:

${ displaystyle {p over 1-p} = e ^ {2 beta JH}}$

damit

${ displaystyle p = {1 über 1 + e ^ {- 2 beta JH}}}$

Der Mittelwert des Spins ergibt sich aus der Mittelung von 1 und -1 mit den Gewichten p und 1 – p, also ist der Mittelwert 2p – 1. Dieser Durchschnitt ist jedoch für alle Drehungen gleich und daher gleich H..

${ displaystyle H = 2p-1 = {1-e ^ {- 2 beta JH} über 1 + e ^ {- 2 beta JH}} = tanh ( beta JH)}$

Die Lösungen für diese Gleichung sind die möglichen konsistenten mittleren Felder. Für βJ. <1 gibt es nur die eine Lösung bei H. = 0. Für größere Werte von β gibt es drei Lösungen und die Lösung bei H. = 0 ist instabil.

Die Instabilität bedeutet, dass ein kleines Erhöhen des mittleren Feldes über Null einen statistischen Anteil von Spins erzeugt, die + sind und größer als der Wert des mittleren Feldes sind. Ein mittleres Feld, das über Null schwankt, erzeugt also ein noch größeres mittleres Feld und setzt sich schließlich an der stabilen Lösung ab. Dies bedeutet, dass für Temperaturen unter dem kritischen Wert βJ. = 1 Das Ising-Modell mit mittlerem Feld durchläuft einen Phasenübergang im Grenzbereich von groß N..

Oberhalb der kritischen Temperatur Schwankungen in H. werden gedämpft, weil das mittlere Feld die Schwankung auf Null zurückstellt. Unterhalb der kritischen Temperatur wird das mittlere Feld auf einen neuen Gleichgewichtswert gebracht, der entweder positiv ist H. oder negativ H. Lösung der Gleichung.

Für βJ. = 1 + ε, knapp unterhalb der kritischen Temperatur, der Wert von H. kann aus der Taylor-Expansion der hyperbolischen Tangente berechnet werden:

${ displaystyle H = tanh ( beta JH) = (1+ varepsilon) H – {(1+ varepsilon) ^ {3} H ^ {3} over 3}}$

Teilen durch H. die instabile Lösung bei zu verwerfen H. = 0, die stabilen Lösungen sind:

${ displaystyle H = { sqrt {3 varepsilon}}}$

Die spontane Magnetisierung H. wächst in der Nähe des kritischen Punktes als Quadratwurzel der Temperaturänderung. Dies gilt immer dann H. kann aus der Lösung einer analytischen Gleichung berechnet werden, die zwischen positiven und negativen Werten symmetrisch ist, was Landau zu dem Verdacht führte, dass alle Phasenübergänge vom Ising-Typ in allen Dimensionen diesem Gesetz folgen sollten.

Der mittlere Feldexponent ist universell, da Änderungen im Charakter von Lösungen analytischer Gleichungen immer durch Katastrophen in der Taylor-Reihe beschrieben werden, bei der es sich um eine Polynomgleichung handelt. Durch Symmetrie ist die Gleichung für H. darf nur ungerade Kräfte von haben H. auf der rechten Seite. Durch Ändern von β sollten die Koeffizienten nur reibungslos geändert werden. Der Übergang erfolgt, wenn der Koeffizient von H. auf der rechten Seite ist 1. In der Nähe des Übergangs:

${ displaystyle H = { partiell ( beta F) über partiell h} = (1 + A varepsilon) H + BH ^ {3} + cdots}$

Wie auch immer EIN und B. Solange keiner von ihnen auf Null eingestellt ist, wächst die spontane Magnetisierung als Quadratwurzel von ε. Dieses Argument kann nur scheitern, wenn die freie Energie βF. ist entweder nicht analytisch oder nicht generisch an dem genauen β, an dem der Übergang stattfindet.

Die spontane Magnetisierung in magnetischen Systemen und die Dichte in Gasen nahe dem kritischen Punkt werden jedoch sehr genau gemessen. Die Dichte und die Magnetisierung in drei Dimensionen haben die gleiche Abhängigkeit des Potenzgesetzes von der Temperatur nahe dem kritischen Punkt, aber das Verhalten aus Experimenten ist:

${ displaystyle H propto varepsilon ^ {0.308}}$

Der Exponent ist ebenfalls universell, da er im Ising-Modell derselbe ist wie im experimentellen Magneten und Gas, aber nicht gleich dem mittleren Feldwert ist. Das war eine große Überraschung.

Dies gilt auch in zwei Dimensionen, wo

${ displaystyle H propto varepsilon ^ {0.125}}$

Aber da war es keine Überraschung, denn es wurde von Onsager vorhergesagt.

Niedrige Abmessungen – Blockdrehungen[edit]

In drei Dimensionen ist die Störreihe aus der Feldtheorie eine Erweiterung einer Kopplungskonstante λ, die nicht besonders klein ist. Die effektive Größe der Kopplung am Fixpunkt beträgt eins über dem Verzweigungsfaktor der Partikelpfade, sodass der Expansionsparameter etwa 1/3 beträgt. In zwei Dimensionen beträgt der störende Expansionsparameter 2/3.

Die Renormierung kann aber auch direkt auf die Spins produktiv angewendet werden, ohne auf ein durchschnittliches Feld überzugehen. Historisch gesehen ist dieser Ansatz auf Leo Kadanoff zurückzuführen und ging der störenden ε-Expansion voraus.

Die Idee ist, Gitterspins iterativ zu integrieren und einen Fluss in Kopplungen zu erzeugen. Aber jetzt sind die Kopplungen Gitterenergiekoeffizienten. Die Tatsache, dass eine Kontinuumsbeschreibung vorhanden ist, garantiert, dass diese Iteration zu einem festen Punkt konvergiert, wenn die Temperatur auf Kritikalität eingestellt wird.

Migdal-Kadanoff-Renormierung[edit]

Schreiben Sie das zweidimensionale Ising-Modell mit einer unendlichen Anzahl möglicher Wechselwirkungen höherer Ordnung. Um die Symmetrie der Spinreflexion aufrechtzuerhalten, tragen nur gleichmäßige Kräfte bei:

${ displaystyle E = sum _ {ij} J_ {ij} S_ {i} S_ {j} + sum J_ {ijkl} S_ {i} S_ {j} S_ {k} S_ {l} ldots.}$

Durch Übersetzungsinvarianz J._ij ist nur eine Funktion von ij. Durch die zufällige Rotationssymmetrie hängt ihre Größe bei i und j nur von der Größe des zweidimensionalen Vektors ab ich – – j. Die Koeffizienten höherer Ordnung sind ebenfalls ähnlich eingeschränkt.

Die Renormierungsiteration teilt das Gitter in zwei Teile – gerade und ungerade Drehungen. Die ungeraden Drehungen leben auf den Gitterpositionen des ungeraden Schachbretts und die geraden auf dem geraden Schachbrett. Wenn die Drehungen durch die Position indiziert sind (ich,j), die ungeraden Seiten sind die mit ich + j ungerade und die geraden Seiten die mit ich + j gerade und gerade Sites sind nur mit ungeraden Sites verbunden.

Die zwei möglichen Werte der ungeraden Drehungen werden durch Summieren über beide möglichen Werte heraus integriert. Dies erzeugt eine neue freie Energiefunktion für die verbleibenden gleichmäßigen Drehungen mit neu eingestellten Kupplungen. Die geraden Drehungen befinden sich wieder in einem Gitter, wobei die Achsen um 45 Grad zu den alten geneigt sind. Durch Deaktivieren des Systems wird die alte Konfiguration wiederhergestellt, jedoch mit neuen Parametern. Diese Parameter beschreiben die Wechselwirkung zwischen Drehungen in Entfernungen

${ displaystyle scriptstyle { sqrt {2}}}$

größer.

Ausgehend vom Ising-Modell und durch Wiederholen dieser Iteration werden schließlich alle Kopplungen geändert. Wenn die Temperatur höher als die kritische Temperatur ist, konvergieren die Kopplungen gegen Null, da die Drehungen in großen Entfernungen nicht korreliert sind. Wenn die Temperatur jedoch kritisch ist, gibt es Koeffizienten ungleich Null, die Spins in allen Ordnungen verbinden. Der Durchfluss kann nur unter Berücksichtigung der ersten Begriffe angenähert werden. Dieser abgeschnittene Fluss erzeugt immer bessere Annäherungen an die kritischen Exponenten, wenn mehr Terme enthalten sind.

Die einfachste Annäherung besteht darin, nur das Übliche beizubehalten J. Begriff, und verwerfen Sie alles andere. Dies erzeugt einen Einfluss J., analog zum einströmen t am festen Punkt von λ in der ε-Expansion.

Um die Änderung in zu finden J.Betrachten Sie die vier Nachbarn einer ungeraden Site. Dies sind die einzigen Drehungen, die damit interagieren. Der multiplikative Beitrag zur Partitionsfunktion aus der Summe über die beiden Werte des Spins an der ungeraden Stelle ist:

${ displaystyle e ^ {J (N _ {+} – N _ {-})} + e ^ {J (N _ {-} – N _ {+})} = 2 cosh (J.[N_{+}-N_{-}])}$

wo N._± ist die Anzahl der Nachbarn, die ± sind. Ohne Berücksichtigung des Faktors 2 beträgt der Beitrag der freien Energie von dieser ungeraden Stelle:

${ displaystyle F = log ( cosh[J(N_{+}-N_{-})]).}$

Dies umfasst erwartungsgemäß Interaktionen mit dem nächsten Nachbarn und dem nächsten Nachbarn, aber auch eine Vier-Spin-Interaktion, die verworfen werden soll. Berücksichtigen Sie zum Abschneiden auf Interaktionen mit dem nächsten Nachbarn, dass der Energiedifferenz zwischen allen Drehungen gleicher und gleicher Anzahl + und – beträgt:

${ displaystyle Delta F = ln ( cosh[4J]).}$

Bei Kopplungen mit dem nächsten Nachbarn beträgt der Energiedifferenz zwischen allen Spins gleich und versetzten Spins 8J.. Die Energiedifferenz zwischen allen Spins gleich und nicht gestaffelt, aber der Netto-Null-Spin beträgt 4J.. Ohne Berücksichtigung von Vier-Spin-Wechselwirkungen ist eine vernünftige Verkürzung der Durchschnitt dieser beiden Energien oder 6J.. Da jeder Link zu zwei ungeraden Drehungen beiträgt, ist der richtige Wert zum Vergleich mit dem vorherigen halb so hoch:

${ displaystyle 3J ‘= ln ( cosh[4J]).}$

Für kleine J.Dies fließt schnell zur Nullkopplung. Groß J ‘s fließen zu großen Kupplungen. Der Magnetisierungsexponent wird aus der Steigung der Gleichung am Fixpunkt bestimmt.

Varianten dieser Methode liefern gute numerische Näherungen für die kritischen Exponenten, wenn viele Terme in zwei und drei Dimensionen enthalten sind.

Anwendungen[edit]

Magnetismus[edit]

Die ursprüngliche Motivation für das Modell war das Phänomen des Ferromagnetismus. Eisen ist magnetisch; Sobald es magnetisiert ist, bleibt es im Vergleich zu jeder Atomzeit lange magnetisiert.

Im 19. Jahrhundert wurde angenommen, dass Magnetfelder auf Ströme in der Materie zurückzuführen sind, und Ampère postulierte, dass Permanentmagnete durch permanente Atomströme verursacht werden. Die Bewegung klassischer geladener Teilchen konnte jedoch keine permanenten Ströme erklären, wie Larmor zeigte. Um Ferromagnetismus zu haben, müssen die Atome permanentmagnetische Momente haben, die nicht auf die Bewegung klassischer Ladungen zurückzuführen sind.

Als der Spin des Elektrons entdeckt wurde, war klar, dass der Magnetismus auf eine große Anzahl von Elektronen zurückzuführen sein sollte, die sich in die gleiche Richtung drehen. Es war natürlich zu fragen, woher die Elektronen alle wissen, in welche Richtung sie sich drehen sollen, da die Elektronen auf der einen Seite eines Magneten nicht direkt mit den Elektronen auf der anderen Seite interagieren. Sie können nur ihre Nachbarn beeinflussen. Das Ising-Modell sollte untersuchen, ob ein großer Teil der Elektronen nur mit lokalen Kräften in die gleiche Richtung gedreht werden kann.

Gittergas[edit]

Das Ising-Modell kann als statistisches Modell für die Bewegung von Atomen neu interpretiert werden. Da die kinetische Energie nur vom Impuls und nicht von der Position abhängt, während die Statistik der Positionen nur von der potentiellen Energie abhängt, hängt die Thermodynamik des Gases nur von der potentiellen Energie für jede Konfiguration von Atomen ab.

Ein grobes Modell besteht darin, Raum-Zeit zu einem Gitter zu machen und sich vorzustellen, dass jede Position entweder ein Atom enthält oder nicht. Der Konfigurationsraum ist der von unabhängigen Bits B._ichwobei jedes Bit entweder 0 oder 1 ist, je nachdem, ob die Position belegt ist oder nicht. Eine attraktive Wechselwirkung reduziert die Energie zweier benachbarter Atome. Wenn die Anziehungskraft nur zwischen den nächsten Nachbarn liegt, wird die Energie um –4 reduziertJB_ichB._j für jedes besetzte Nachbarpaar.

Die Dichte der Atome kann durch Hinzufügen eines chemischen Potentials gesteuert werden, was multiplikative Wahrscheinlichkeitskosten für das Hinzufügen eines weiteren Atoms darstellt. Ein multiplikativer Wahrscheinlichkeitsfaktor kann als additiver Term im Logarithmus – der Energie – neu interpretiert werden. Die zusätzliche Energie einer Konfiguration mit N. Atome wird verändert durch μN. Die Wahrscheinlichkeitskosten eines weiteren Atoms sind ein Faktor von exp (-βμ).

Die Energie des Gittergases ist also:

${ displaystyle E = – { frac {1} {2}} sum _ { langle i, j rangle} 4JB_ {i} B_ {j} + sum _ {i} mu B_ {i}}$

Umschreiben der Bits in Form von Drehungen,

${ displaystyle B_ {i} = (S_ {i} +1) / 2.}$

${ displaystyle E = – { frac {1} {2}} sum _ { langle i, j rangle} JS_ {i} S_ {j} – { frac {1} {2}} sum _ {i} (4J- mu) S_ {i}}$

Für Gitter, bei denen jeder Standort die gleiche Anzahl von Nachbarn hat, ist dies das Ising-Modell mit einem Magnetfeld h = (zJ – – μ) / 2, wo z ist die Anzahl der Nachbarn.

In biologischen Systemen wurden modifizierte Versionen des Gittergasmodells verwendet, um eine Reihe von Bindungsverhalten zu verstehen. Dazu gehört die Bindung von Liganden an Rezeptoren in der Zelloberfläche,^[25] die Bindung von Chemotaxis-Proteinen an den Flagellenmotor,^[26] und die Kondensation von DNA.^[27]

Anwendung auf die Neurowissenschaften[edit]

Die Aktivität von Neuronen im Gehirn kann statistisch modelliert werden. Jedes Neuron ist zu jeder Zeit entweder aktiv + oder inaktiv -. Die aktiven Neuronen sind diejenigen, die in einem bestimmten Zeitfenster ein Aktionspotential über das Axon senden, und die inaktiven sind diejenigen, die dies nicht tun. Da die neuronale Aktivität zu jedem Zeitpunkt durch unabhängige Bits modelliert wird, schlug Hopfield vor, dass ein dynamisches Ising-Modell eine erste Annäherung an ein lernfähiges neuronales Netzwerk liefern würde.^[28]

Nach dem allgemeinen Ansatz von Jaynes,^[29][30] eine aktuelle Interpretation von Schneidman, Berry, Segev und Bialek,^[31]
ist, dass das Ising-Modell für jedes Modell der neuronalen Funktion nützlich ist, da ein statistisches Modell für die neuronale Aktivität nach dem Prinzip der maximalen Entropie gewählt werden sollte. Bei einer Sammlung von Neuronen führt ein statistisches Modell, das die durchschnittliche Feuerrate für jedes Neuron reproduzieren kann, einen Lagrange-Multiplikator für jedes Neuron ein:

${ displaystyle E = – sum _ {i} h_ {i} S_ {i}}$

Die Aktivität jedes Neurons in diesem Modell ist jedoch statistisch unabhängig. Um Paarkorrelationen zu berücksichtigen, führen Sie paarweise Lagrange-Multiplikatoren ein, wenn ein Neuron dazu neigt, zusammen mit einem anderen zu feuern (oder nicht zu feuern):

${ displaystyle E = – { tfrac {1} {2}} sum _ {ij} J_ {ij} S_ {i} S_ {j} – sum _ {i} h_ {i} S_ {i}}$

wo

${ displaystyle J_ {ij}}$

sind nicht auf Nachbarn beschränkt. Beachten Sie, dass diese Verallgemeinerung des Ising-Modells in der Statistik manchmal als quadratische exponentielle Binärverteilung bezeichnet wird. Diese Energiefunktion führt nur Wahrscheinlichkeitsverzerrungen für einen Spin mit einem Wert und für ein Paar von Spins mit demselben Wert ein. Korrelationen höherer Ordnung werden von den Multiplikatoren nicht eingeschränkt. Ein Aktivitätsmuster, das aus dieser Verteilung abgetastet wird, erfordert die größte Anzahl von Bits, um in einem Computer gespeichert zu werden, und zwar im effizientesten vorstellbaren Codierungsschema, verglichen mit jeder anderen Verteilung mit derselben durchschnittlichen Aktivität und paarweisen Korrelationen. Dies bedeutet, dass Ising-Modelle für jedes System relevant sind, das durch möglichst zufällige Bits beschrieben wird, wobei die paarweisen Korrelationen und die durchschnittliche Anzahl von Einsen, die sowohl in den Natur- als auch in den Sozialwissenschaften häufig vorkommen, eingeschränkt sind.

Gläser drehen[edit]

Mit dem Ising-Modell können auch die sogenannten Spin-Gläser durch den üblichen Hamilton-Operator beschrieben werden

${ displaystyle { hat {H}} = – { frac {1} {2}} , sum J_ {i, k} , S_ {i} , S_ {k},}$

bei dem die S.-Variablen beschreiben die Ising-Drehungen, während die J._{ich k} werden aus einer zufälligen Verteilung entnommen. Für Spingläser wählt eine typische Verteilung mit Wahrscheinlichkeit antiferromagnetische Bindungen p und ferromagnetische Bindungen mit der Wahrscheinlichkeit 1 – p. Diese Anleihen bleiben fest oder “gelöscht” auch bei thermischen Schwankungen. Wann p = 0 wir haben das ursprüngliche Ising-Modell. Dieses System verdient ein eigenes Interesse. vor allem hat man “nicht ergodisch” Eigenschaften, die zu seltsamem Entspannungsverhalten führen. Viel Aufmerksamkeit wurde auch durch das verwandte Ising-Modell für gebundene und ortsverdünnte Ising erregt, insbesondere in zwei Dimensionen, was zu einem faszinierenden kritischen Verhalten führte.^[32]

Meeres-Eis[edit]

2D-Schmelzteichnäherungen können mithilfe des Ising-Modells erstellt werden. Die Daten der Meereistopographie wirken sich ziemlich stark auf die Ergebnisse aus. Die Zustandsvariable ist für eine einfache 2D-Näherung binär und besteht entweder aus Wasser oder Eis.^[33]

Siehe auch[edit]

1. ^ Siehe Gallavotti (1999), Kapitel VI-VII.
2. ^ Ernst Ising, Beitrag zur Theorie des Ferromagnetismus
3. ^ https://www.springer.com/gp/book/9783642152016, https://www.springer.com/gp/book/9781461462880
4. ^ Siehe Baierlein (1999), Kapitel 16.
5. ^ Barahona, Francisco; Grötschel, Martin; Jünger, Michael; Reinelt, Gerhard (1988). “Eine Anwendung der kombinatorischen Optimierung auf die statistische Physik und das Schaltungslayoutdesign”. Unternehmensforschung. 36 (3): 493–513. doi:10.1287 / opre.36.3.493. ISSN 0030-364X. JSTOR 170992.
6. ^ El-Showk, Sheer; Paulos, Miguel F.; Polen, David; Rychkov, Slava; Simmons-Duffin, David; Vichi, Alessandro (2014). “Lösen des 3D-Ising-Modells mit dem Conformal Bootstrap II. C-Minimierung und präzise kritische Exponenten” (PDF). Zeitschrift für Statistische Physik. 157 (4–5): 869–914. arXiv:1403,4545. Bibcode:2014JSP … 157..869E. doi:10.1007 / s10955-014-1042-7. S2CID 119627708. Archiviert von das Original (PDF) am 07.04.2014. Abgerufen 2013-04-21.
7. ^ Peierls, R.; Geboren M. (1936). “Nach Isings Modell des Ferromagnetismus”. Mathematische Verfahren der Cambridge Philosophical Society. 32 (3): 477. Bibcode:1936PCPS … 32..477P. doi:10.1017 / S0305004100019174.
8. ^ ^{ein b c} Montroll, Potts & Ward 1963, S. 308–309
9. ^ ^{ein b c d e f G h ich j} Newman M.E.J., Barkema G.T., “Monte-Carlo-Methoden in der statistischen Physik”Clarendon Press, 1999.
10. ^ Teif, Vladimir B. (2007). “Allgemeiner Transfermatrix-Formalismus zur Berechnung der DNA-Protein-Wirkstoff-Bindung bei der Genregulation”. Nucleic Acids Res. 35 (11): e80. doi:10.1093 / nar / gkm268. PMC 1920246. PMID 17526526.
11. ^ ^{ein b} Ruelle (1969). Statistische Mechanik: Rigorose Ergebnisse. New York: WA Benjamin Inc.
12. ^ Dyson, FJ (1969). “Existenz eines Phasenübergangs in einem eindimensionalen Ising-Ferromagneten”. Comm. Mathematik. Phys. 12 (2): 91–107. Bibcode:1969CMaPh..12 … 91D. doi:10.1007 / BF01645907. S2CID 122117175.
13. ^ Fröhlich, J.; Spencer, T. (1982). “Der Phasenübergang im eindimensionalen Ising-Modell mit 1 /r² Wechselwirkungsenergie”. Comm. Mathematik. Phys. 84 (1): 87–101. Bibcode:1982CMaPh..84 … 87F. doi:10.1007 / BF01208373. S2CID 122722140.
14. ^ Baxter, Rodney J. (1982), Genau gelöste Modelle in der statistischen Mechanik, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, HERR 0690578, archiviert von das Original am 20.03.2012abgerufen 2009-10-25
15. ^ Suzuki, Sei; Inoue, Jun-ichi; Chakrabarti, Bikas K. (2012). Quantenisierungsphasen und -übergänge in transversalen Isingmodellen. Springer. doi:10.1007 / 978-3-642-33039-1. ISBN 978-3-642-33038-4.
16. ^ Holz, Charlie. “Das Cartoon-Bild von Magneten, die die Wissenschaft verändert haben”. Quanta Magazine. Abgerufen 2020-06-26.
17. ^ “SIAM: Das Ising-Modell ist NP-vollständig”. archive.siam.org. Abgerufen 2020-06-26.
18. ^ Billó, M.; Caselle, M.; Gaiotto, D.; Gliozzi, F.; Meineri, M.; andere (2013). “Linienfehler im 3D-Ising-Modell”. JHEP. 1307 (7): 055. arXiv:1304.4110. Bibcode:2013JHEP … 07..055B. doi:10.1007 / JHEP07 (2013) 055. S2CID 119226610.
19. ^ Cosme, Catarina; Lopes, JM Viana Parente; Penedones, Joao (2015). “Konforme Symmetrie des kritischen 3D-Ising-Modells innerhalb einer Kugel”. Zeitschrift für Hochenergiephysik. 2015 (8): 22. arXiv:1503.02011. Bibcode:2015JHEP … 08..022C. doi:10.1007 / JHEP08 (2015) 022. S2CID 53710971.
20. ^ Delamotte, Bertrand; Tissier, Matthieu; Wschebor, Nicolás (2016). “Die Skaleninvarianz impliziert eine konforme Invarianz für das dreidimensionale Ising-Modell”. Körperliche Überprüfung E.. 93 (12144): 012144. arXiv:1501.01776. Bibcode:2016PhRvE..93a2144D. doi:10.1103 / PhysRevE.93.012144. PMID 26871060. S2CID 14538564.
21. ^ El-Showk, Sheer; Paulos, Miguel F.; Polen, David; Rychkov, Slava; Simmons-Duffin, David; Vichi, Alessandro (2012). “Lösen des 3D-Ising-Modells mit dem konformen Bootstrap”. Phys. Rev.. D86 (2): 025022. arXiv:1203.6064. Bibcode:2012PhRvD..86b5022E. doi:10.1103 / PhysRevD.86.025022. S2CID 39692193.
22. ^ El-Showk, Sheer; Paulos, Miguel F.; Polen, David; Rychkov, Slava; Simmons-Duffin, David; Vichi, Alessandro (2014). “Lösen des 3D-Ising-Modells mit dem Conformal Bootstrap II. c-Minimierung und präzise kritische Exponenten”. Zeitschrift für Statistische Physik. 157 (4–5): 869–914. arXiv:1403,4545. Bibcode:2014JSP … 157..869E. doi:10.1007 / s10955-014-1042-7. S2CID 119627708.
23. ^ Simmons-Duffin, David (2015). “Ein semidefiniter Programmlöser für den konformen Bootstrap”. Zeitschrift für Hochenergiephysik. 2015 (6): 174. arXiv:1502.02033. Bibcode:2015JHEP … 06..174S. doi:10.1007 / JHEP06 (2015) 174. ISSN 1029-8479. S2CID 35625559.
24. ^ Kadanoff, Leo P. (30. April 2014). “Tiefes Verständnis für das 3D-Ising-Modell”. Journal Club für Festkörperphysik. Archiviert von das Original am 22. Juli 2015. Abgerufen 19. Juli 2015.
25. ^ Shi, Y.; Duke, T. (1998-11-01). “Kooperatives Modell der Bakterienerkennung”. Körperliche Überprüfung E.. 58 (5): 6399–6406. arXiv:Physik / 9901052. Bibcode:1998PhRvE..58.6399S. doi:10.1103 / PhysRevE.58.6399. S2CID 18854281.
26. ^ Bai, Fan; Branch, Richard W.; Nicolau, Dan V.; Pilizota, Teuta; Steel, Bradley C.; Maini, Philip K.; Berry, Richard M. (05.02.2010). “Konformationsausbreitung als Mechanismus für die Kooperativität im bakteriellen Flagellenschalter”. Wissenschaft. 327 (5966): 685–689. Bibcode:2010Sci … 327..685B. doi:10.1126 / science.1182105. ISSN 0036-8075. PMID 20133571. S2CID 206523521.
27. ^ Vtyurina, Natalia N.; Dulin, David; Docter, Margreet W.; Meyer, Anne S.; Dekker, Nynke H.; Abbondanzieri, Elio A. (18.04.2016). “Die Hysterese bei der DNA-Verdichtung durch Dps wird durch ein Ising-Modell beschrieben”. Verfahren der Nationalen Akademie der Wissenschaften. 113 (18): 4982–7. Bibcode:2016PNAS..113.4982V. doi:10.1073 / pnas.1521241113. ISSN 0027-8424. PMC 4983820. PMID 27091987.
28. ^ JJ Hopfield (1982), “Neuronale Netze und physikalische Systeme mit neuen kollektiven Rechenfähigkeiten”, Verfahren der National Academy of Sciences der USA, 79 (8): 2554–2558, Bibcode:1982PNAS … 79.2554H, doi:10.1073 / pnas.79.8.2554, PMC 346238, PMID 6953413.
29. ^ Jaynes, ET (1957), “Informationstheorie und statistische Mechanik”, Körperliche Überprüfung, 106 (4): 620–630, Bibcode:1957PhRv..106..620J, doi:10.1103 / PhysRev.106.620, S2CID 17870175.
30. ^ Jaynes, Edwin T. (1957), “Informationstheorie und statistische Mechanik II”, Körperliche Überprüfung, 108 (2): 171–190, Bibcode:1957PhRv..108..171J, doi:10.1103 / PhysRev.108.171.
31. ^ Elad Schneidman; Michael J. Berry; Ronen Segev; William Bialek (2006), “Schwache paarweise Korrelationen implizieren stark korrelierte Netzwerkzustände in einer neuronalen Population”, Natur, 440 (7087): 1007–1012, arXiv:q-bio / 0512013, Bibcode:2006Natur.440.1007S, doi:10.1038 / nature04701, PMC 1785327, PMID 16625187.
32. ^ JS Wang, W. Selke, VB Andreichenko und VS Dotsenko (1990), “Das kritische Verhalten des zweidimensionalen verdünnten Modells”, Physica A., 164 (2): 221–239, Bibcode:1990PhyA..164..221W, doi:10.1016 / 0378-4371 (90) 90196-YCS1-Wartung: mehrere Namen: Autorenliste (Link)
33. ^ Yi-Ping Ma; Ivan Sudakov; Courtenay stark; Kenneth Golden (2017), Ising Modell für Schmelzteiche auf arktischem Meereis, arXiv:1408.2487v3

Verweise[edit]

• Baxter, Rodney J. (1982), Genau gelöste Modelle in der statistischen Mechanik, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, HERR 0690578
• K. Binder (2001) [1994], “Ising Modell”, Enzyklopädie der Mathematik, EMS Press
• Stephen G. Brush (1967), Geschichte des Lenz-Ising-Modells. Rezensionen der modernen Physik (American Physical Society) vol. 39, S. 883–893. (10.1103 / RevModPhys.39.883)
• Baierlein, R. (1999), Thermische Physik, Cambridge: Cambridge University Press, ISBN 978-0-521-59082-2
• Gallavotti, G. (1999), Statistische Mechanik, Texte und Monographien in Physik, Berlin: Springer-Verlag, doi:10.1007 / 978-3-662-03952-6, ISBN 978-3-540-64883-3, HERR 1707309
• Huang, Kerson (1987), Statistische Mechanik (2. Auflage), Wiley, ISBN 978-0-471-81518-1
• Ising, E. (1925), “Beitrag zur Theorie des Ferromagnetismus”, Z. Phys., 31 (1): 253–258, Bibcode:1925ZPhy … 31..253I, doi:10.1007 / BF02980577, S2CID 122157319
• Itzykson, Claude; Drouffe, Jean-Michel (1989), Théorie statistique des champs, Band 1, Savoirs Actuels (CNRS), EDV Sciences Editions, ISBN 978-2-86883-360-0
• Itzykson, Claude; Drouffe, Jean-Michel (1989), Statistische Feldtheorie, Band 1: Von der Brownschen Bewegung zur Renormierung und Gittermaßtheorie, Cambridge University Press, ISBN 978-0-521-40805-9
• Friedli, S.; Velenik, Y. (2017). Statistische Mechanik von Gittersystemen: eine konkrete mathematische Einführung. Cambridge: Cambridge University Press. ISBN 9781107184824.
• Ross Kindermann und J. Laurie Snell (1980), Markov-Zufallsfelder und ihre Anwendungen. Amerikanische Mathematische Gesellschaft. ISBN 0-8218-3381-2.
• Kleinert, H (1989), Messfelder in kondensierter MaterieVol. ICH, “Superflow- und Vortex-Linien”S. 1–742, Bd. II, “Belastungen und Mängel”S. 743–1456, World Scientific (Singapur);; Taschenbuch ISBN 9971-5-0210-0 (auch online verfügbar: Vol. ich und Vol. II)
• Kleinert, H und Schulte-Frohlinde, V (2001), Kritische Eigenschaften von φ⁴-Theorien, World Scientific (Singapur);; Taschenbuch ISBN 981-02-4658-7 (auch verfügbar online)
• Lenz, W. (1920), “Beiträge zum Verständnis der magnetischen Eigenschaften in festen Körpern”, Physikalische Zeitschrift, 21: 613–615.
• Barry M. McCoy und Tai Tsun Wu (1973), Das zweidimensionale Ising-Modell. Harvard University Press, Cambridge, Massachusetts, ISBN 0-674-91440-6
• Montroll, Elliott W.; Potts, Renfrey B.; Ward, John C. (1963), “Korrelationen und spontane Magnetisierung des zweidimensionalen Ising-Modells”, Zeitschrift für Mathematische Physik, 4 (2): 308–322, Bibcode:1963JMP ….. 4..308M, doi:10.1063 / 1.1703955, ISSN 0022-2488, HERR 0148406, archiviert von das Original am 12.01.2013
• Onsager, Lars (1944), “Kristallstatistik. I. Ein zweidimensionales Modell mit einem Ordnungsstörungsübergang”, Körperliche Überprüfung, Serie II, 65 (3–4): 117–149, Bibcode:1944PhRv … 65..117O, doi:10.1103 / PhysRev.65.117, HERR 0010315
• Onsager, Lars (1949), “Diskussion”, Nuovo Cimento Supplement, 6: 261
• John Palmer (2007), Planare Ising-Korrelationen. Birkhäuser, Boston, ISBN 978-0-8176-4248-8.
• Istrail, Sorin (2000), “Statistische Mechanik, Dreidimensionalität und NP-Vollständigkeit. I. Universalität der Unlösbarkeit für die Partitionsfunktion des Ising-Modells über nichtplanare Oberflächen (erweiterte Zusammenfassung)” (PDF), Vorträge des zweiunddreißigsten jährlichen ACM-Symposiums zur Theorie des Rechnens, ACM, S. 87–96, doi:10.1145 / 335305.335316, ISBN 978-1581131840, HERR 2114521, S2CID 7944336
• Yang, CN (1952), “Die spontane Magnetisierung eines zweidimensionalen Ising-Modells”, Körperliche Überprüfung, Serie II, 85 (5): 808–816, Bibcode:1952PhRv … 85..808Y, doi:10.1103 / PhysRev.85.808, HERR 0051740

Externe Links[edit]