Integral – Wikipedia

Operation im Kalkül

Ein bestimmtes Integral einer Funktion kann als vorzeichenbehafteter Bereich des durch seinen Graphen begrenzten Bereichs dargestellt werden.

In der Mathematik ist ein Integral- Weist Funktionen Funktionen so zu, dass sie Verschiebung, Fläche, Volumen und andere Konzepte beschreiben können, die durch die Kombination von infinitesimalen Daten entstehen. Der Prozess des Findens von Integralen wird aufgerufen Integration. Integration ist neben Differenzierung eine grundlegende Operation der Analysis,^[a] und dient als Werkzeug zur Lösung von Problemen in Mathematik und Physik, die unter anderem den Bereich einer beliebigen Form, die Länge einer Kurve und das Volumen eines Festkörpers betreffen.

Die in diesem Artikel behandelten Integrale werden als solche bezeichnet bestimmte IntegraleDies kann formal als der vorzeichenbehaftete Bereich der Region in der Ebene interpretiert werden, der durch den Graphen einer bestimmten Funktion zwischen zwei Punkten in der realen Linie begrenzt wird. Integrale können sich auch auf das Konzept eines Antiderivativs beziehen, einer Funktion, deren Ableitung die gegebene Funktion ist. In diesem Fall werden sie aufgerufen unbestimmte Integrale. Der Grundsatz des Kalküls verknüpft bestimmte Integrale mit Differenzierung und bietet eine Methode zur Berechnung des bestimmten Integrals einer Funktion, wenn ihr Antiderivativ bekannt ist.

Obwohl Methoden zur Berechnung von Flächen und Volumina aus der antiken griechischen Mathematik stammen, wurden die Integrationsprinzipien im späten 17. Jahrhundert von Isaac Newton und Gottfried Wilhelm Leibniz unabhängig formuliert, die die Fläche unter einer Kurve als unendliche Summe von Rechtecken infinitesimaler Breite betrachteten . Bernhard Riemann gab später eine strenge Definition von Integralen, die auf einem Begrenzungsverfahren basiert, das die Fläche eines krummlinigen Bereichs durch Aufteilen des Bereichs in dünne vertikale Platten approximiert.

Integrale können abhängig vom Typ der Funktion sowie der Domäne, über die die Integration durchgeführt wird, verallgemeinert werden. Beispielsweise wird ein Linienintegral für Funktionen von zwei oder mehr Variablen definiert, und das Integrationsintervall wird durch eine Kurve ersetzt, die die beiden Endpunkte des Intervalls verbindet. In einem Oberflächenintegral wird die Kurve durch ein Stück einer Oberfläche im dreidimensionalen Raum ersetzt.

Geschichte[edit]

Pre-Calculus-Integration[edit]

Die erste dokumentierte systematische Technik zur Bestimmung von Integralen ist die Erschöpfungsmethode des antiken griechischen Astronomen Eudoxus (Ca. 370 v. Chr.), Die nach Gebieten und Volumen suchten, indem sie in eine unendliche Anzahl von Abteilungen aufgeteilt wurden, für die das Gebiet oder Volumen bekannt war.^[1] Diese Methode wurde von Archimedes im 3. Jahrhundert v. Chr. Weiterentwickelt und angewendet und zur Berechnung der Fläche eines Kreises, der Oberfläche und des Volumens einer Kugel, der Fläche einer Ellipse, der Fläche unter einer Parabel und des Volumens eines Segments von verwendet ein Rotationsparaboloid, das Volumen eines Segments eines Rotationshyperboloids und die Fläche einer Spirale.^[2]

Eine ähnliche Methode wurde in China um das 3. Jahrhundert n. Chr. Unabhängig von Liu Hui entwickelt, der damit die Fläche des Kreises fand. Diese Methode wurde später im 5. Jahrhundert von den chinesischen Vater-Sohn-Mathematikern Zu Chongzhi und Zu Geng verwendet, um das Volumen einer Kugel zu ermitteln.^[3]

Im Nahen Osten Hasan Ibn al-Haytham, latinisiert als Alhazen (c.965 – c.1040 AD) leitete eine Formel für die Summe der vierten Potenzen ab.^[4] Er verwendete die Ergebnisse, um eine so genannte Integration dieser Funktion durchzuführen, wobei die Formeln für die Summen der Integralquadrate und der vierten Potenzen es ihm ermöglichten, das Volumen eines Paraboloids zu berechnen.^[5]

Die nächsten bedeutenden Fortschritte in der Integralrechnung zeigten sich erst im 17. Jahrhundert. Zu dieser Zeit begann die Arbeit von Cavalieri mit seiner Methode der Unteilbarkeit und die Arbeit von Fermat den Grundstein für die moderne Analysis zu legen.^[6] mit Cavalieri Berechnung der Integrale von xⁿ bis zu einem gewissen Grad n = 9 in Cavalieris Quadraturformel.^[7] Weitere Schritte wurden im frühen 17. Jahrhundert von Barrow und Torricelli unternommen, die die ersten Hinweise auf einen Zusammenhang zwischen Integration und Differenzierung lieferten. Barrow lieferte den ersten Beweis für den Grundsatz der Analysis.^[8]Wallis verallgemeinerte Cavalieris Methode und berechnete Integrale von x zu einer allgemeinen Macht, einschließlich negativer Kräfte und gebrochener Kräfte.^[9]

Leibniz und Newton[edit]

Der größte Fortschritt in der Integration erfolgte im 17. Jahrhundert mit der unabhängigen Entdeckung des Grundsatzes der Analysis durch Leibniz und Newton.^[10] Der Satz zeigt einen Zusammenhang zwischen Integration und Differenzierung. Diese Verbindung kann in Kombination mit der vergleichsweise einfachen Differenzierung zur Berechnung von Integralen genutzt werden. Insbesondere der Grundsatz der Analysis erlaubt es, eine viel breitere Klasse von Problemen zu lösen. Ebenso wichtig ist der umfassende mathematische Rahmen, den sowohl Leibniz als auch Newton entwickelt haben. Unter dem Namen Infinitesimalrechnung ermöglichte es eine genaue Analyse von Funktionen in kontinuierlichen Domänen. Dieser Rahmen wurde schließlich zu einem modernen Kalkül, dessen Notation für Integrale direkt aus der Arbeit von Leibniz stammt.

Formalisierung[edit]

Während Newton und Leibniz einen systematischen Ansatz für die Integration lieferten, fehlte ihrer Arbeit ein gewisses Maß an Genauigkeit. Bischof Berkeley griff denkwürdigerweise die von Newton verwendeten verschwindenden Schritte an und nannte sie “Geister von abgereisten Mengen”.^[11] Mit der Entwicklung von Grenzen wurde Calculus fester. Die Integration wurde zunächst von Riemann rigoros unter Verwendung von Grenzen formalisiert.^[12] Obwohl alle begrenzten stückweise stetigen Funktionen in einem begrenzten Intervall Riemann-integrierbar sind, wurden später allgemeinere Funktionen betrachtet – insbesondere im Kontext der Fourier-Analyse -, für die Riemanns Definition nicht gilt, und Lebesgue formulierte eine andere Definition des Integrals, die auf Maß basiert Theorie (ein Teilfeld der realen Analyse). Andere Definitionen von Integral, die die Ansätze von Riemann und Lebesgue erweitern, wurden vorgeschlagen. Diese auf dem reellen Zahlensystem basierenden Ansätze sind heute die gebräuchlichsten, es gibt jedoch alternative Ansätze, beispielsweise eine Definition des Integrals als Standardteil einer unendlichen Riemannschen Summe, die auf dem hyperrealen Zahlensystem basiert.

Historische Notation[edit]

Die Notation für das unbestimmte Integral wurde 1675 von Gottfried Wilhelm Leibniz eingeführt.^[13] Er passte das integrale Symbol an, ∫aus dem Brief ſ (lange s), steht für summa (geschrieben als ſumma;; Latein für “Summe” oder “gesamt”). Die moderne Notation für das bestimmte Integral mit Grenzen über und unter dem Integralzeichen wurde erstmals von Joseph Fourier in verwendet Mémoires der französischen Akademie um 1819–20, abgedruckt in seinem Buch von 1822.^[14]

Isaac Newton verwendete einen kleinen vertikalen Balken über einer Variablen, um die Integration anzuzeigen, oder platzierte die Variable in einem Feld. Die vertikale Leiste war leicht zu verwechseln .x oder x‘, die zur Unterscheidung verwendet werden, und die Box-Notation war für Drucker schwer zu reproduzieren, so dass diese Notationen nicht weit verbreitet waren.^[15]

Erste Verwendung des Begriffs[edit]

Der Begriff wurde erstmals 1690 von Jacob Bernoulli in lateinischer Sprache gedruckt: “Ergo et horum Integralia aequantur”.^[16]

Terminologie und Notation[edit]

Im Allgemeinen das Integral einer reellen Funktion f((x) in Bezug auf eine reale Variable x in einem Intervall [a, b] ist geschrieben als

${ displaystyle int _ {a} ^ {b} f (x) , dx.}$

Das Integralzeichen ∫ steht für Integration. (In der modernen arabischen mathematischen Notation ein reflektiertes Integralsymbol wird eingesetzt.^[17]) Das Symbol dx, genannt das Differential der Variablen xgibt an, dass die Integrationsvariable ist x. Die Funktion f((x) heißt der Integrand, die Punkte ein und b werden die Integrationsgrenzen genannt, und das Integral soll über dem Intervall liegen [a, b], genannt das Integrationsintervall.^[18] Eine Funktion wird als integrierbar bezeichnet, wenn das Integral über ihre Domäne endlich ist, und wenn die Grenzen angegeben sind, wird das Integral als bestimmtes Integral bezeichnet.

Wenn die Grenzen weggelassen werden, wie in

${ displaystyle int f (x) , dx,}$

Das Integral wird als unbestimmtes Integral bezeichnet, das eine Klasse von Funktionen (das Antiderivativ) darstellt, deren Ableitung der Integrand ist.^[19] Der Grundsatz der Analysis bezieht die Bewertung bestimmter Integrale auf unbestimmte Integrale. Es gibt verschiedene Erweiterungen der Notation für Integrale, die die Integration in unbegrenzten Domänen und / oder in mehreren Dimensionen umfassen (siehe spätere Abschnitte dieses Artikels).

In erweiterten Einstellungen ist es nicht ungewöhnlich, dass Sie darauf verzichten dx wenn nur das einfache Riemannsche Integral verwendet wird oder die genaue Art des Integrals unerheblich ist. Zum Beispiel könnte man schreiben

um die Linearität des Integrals auszudrücken, eine Eigenschaft, die das Riemannsche Integral und alle Verallgemeinerungen davon teilen.^[20]

Interpretationen[edit]

Annäherungen an das Integral von √x von 0 bis 1 mit 5 gelben rechten Endpunktpartitionen und 12 grünen linken Endpunktpartitionen

Integrale treten in vielen praktischen Situationen auf. Zum Beispiel kann man aus der Länge, Breite und Tiefe eines rechteckigen Schwimmbades mit flachem Boden das darin enthaltene Wasservolumen, die Fläche seiner Oberfläche und die Länge seiner Kante bestimmen. Wenn es jedoch oval mit abgerundetem Boden ist, sind Integrale erforderlich, um genaue und strenge Werte für diese Größen zu finden. In jedem Fall kann man die gesuchte Menge in unendlich viele infinitesimale Stücke teilen und dann die Stücke summieren, um eine genaue Annäherung zu erreichen.

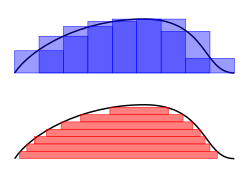
Zum Beispiel, um den Bereich des Bereichs zu finden, der durch den Funktionsgraphen begrenzt ist f((x) = √x zwischen x = 0 und x = 1kann man das Intervall in fünf Schritten überqueren (0, 1/5, 2/5, …, 1), dann füllen Sie ein Rechteck mit der rechten Endhöhe jedes Stücks (also √0, √1/5, √2/5, …, √1) und summieren ihre Flächen, um eine Annäherung an zu erhalten

${ displaystyle textstyle { sqrt { frac {1} {5}}} left ({ frac {1} {5}} – 0 right) + { sqrt { frac {2} {5} }} left ({ frac {2} {5}} – { frac {1} {5}} right) + cdots + { sqrt { frac {5} {5}}} left ( { frac {5} {5}} – { frac {4} {5}} right) ca. 0,7497,}$

Das ist größer als der genaue Wert. Wenn Sie diese Teilintervalle durch solche mit der linken Endhöhe jedes Stücks ersetzen, ist alternativ die Annäherung zu niedrig: Bei zwölf solchen Teilintervallen beträgt die angenäherte Fläche nur 0,6203. Wenn jedoch die Anzahl der Teile auf unendlich ansteigt, erreicht sie eine Grenze, die der genaue Wert der gesuchten Fläche ist (in diesem Fall 2/3). Man schreibt

${ displaystyle int _ {0} ^ {1} { sqrt {x}} , dx = { frac {2} {3}},}$

was bedeutet 2/3 ist das Ergebnis einer gewichteten Summe von Funktionswerten, √x, multipliziert mit den infinitesimalen Schrittbreiten, bezeichnet mit dxauf das Intervall [0, 1].

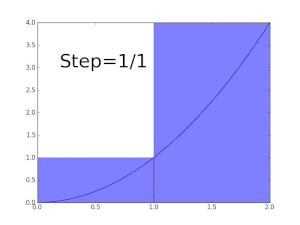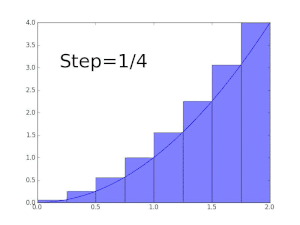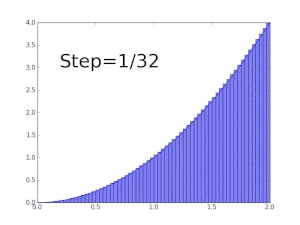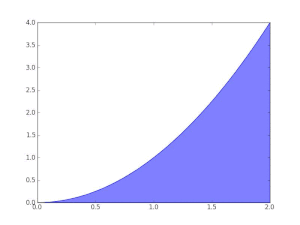
Darboux obere Summen der Funktion y = x²

Darboux niedrigere Summen der Funktion y = x²

Formale Definitionen[edit]

Es gibt viele Möglichkeiten, ein Integral formal zu definieren, von denen nicht alle gleichwertig sind. Die Unterschiede bestehen hauptsächlich darin, unterschiedliche Sonderfälle zu behandeln, die unter anderen Definitionen möglicherweise nicht integrierbar sind, aber gelegentlich auch aus pädagogischen Gründen. Die am häufigsten verwendeten Definitionen sind Riemann-Integrale und Lebesgue-Integrale.

Riemann-Integral[edit]

Das Riemannsche Integral ist definiert als Riemannsche Funktionssummen in Bezug auf getaggte Partitionen eines Intervalls.^[21] Eine markierte Partition eines geschlossenen Intervalls [a, b] auf der realen Linie ist eine endliche Folge

${ displaystyle a = x_ {0} leq t_ {1} leq x_ {1} leq t_ {2} leq x_ {2} leq cdots leq x_ {n-1} leq t_ {n } leq x_ {n} = b. , !}$

Dadurch wird das Intervall aufgeteilt [a, b] in n Unterintervalle [x_i−1, x_i] indiziert von ich, von denen jeder ist “getaggt” mit einem besonderen Punkt t_ich ∈ [x_i−1, x_i]. EIN Riemannsumme einer Funktion f in Bezug auf eine solche markierte Partition ist definiert als

${ displaystyle sum _ {i = 1} ^ {n} f (t_ {i}) , Delta _ {i};}$

Somit ist jeder Term der Summe die Fläche eines Rechtecks ​​mit einer Höhe, die dem Funktionswert am bestimmten Punkt des gegebenen Unterintervalls entspricht, und einer Breite, die der Breite des Unterintervalls entspricht. Δ_ich = x_ich– –x_ich−1. Das Gittergewebe einer solchen markierten Partition ist die Breite des größten von der Partition gebildeten Teilintervalls. max_{ich= 1 …n} Δ_ich. Das Riemann-Integral einer Funktion f über das Intervall [a, b] entspricht S. wenn:^[22]

Für alle ε > 0 es gibt δ > 0 so dass für jede markierte Partition [a, b] mit Maschenweite weniger als δ,

${ displaystyle left | S- sum _ {i = 1} ^ {n} f (t_ {i}) , Delta _ {i} right | < varepsilon.}$

Wenn die ausgewählten Tags den maximalen (bzw. minimalen) Wert jedes Intervalls angeben, wird die Riemann-Summe zu einer oberen (bzw. unteren) Darboux-Summe, was auf die enge Verbindung zwischen dem Riemann-Integral und dem Darboux-Integral hindeutet.

Lebesgue-Integral[edit]

Riemann-Darboux-Integration (oben) und Lebesgue-Integration (unten)

Sowohl in der Theorie als auch in der Anwendung ist es oft von Interesse, an die Grenze unter dem Integral gelangen zu können. Beispielsweise kann häufig eine Folge von Funktionen konstruiert werden, die in geeigneter Weise die Lösung eines Problems annähern. Dann sollte das Integral der Lösungsfunktion die Grenze der Integrale der Approximationen sein. Viele Funktionen, die als Grenzen erhalten werden können, sind jedoch nicht Riemann-integrierbar, so dass solche Grenzwertsätze nicht mit dem Riemann-Integral gelten. Daher ist es von großer Bedeutung, eine Definition des Integrals zu haben, die die Integration einer breiteren Klasse von Funktionen ermöglicht.^[23]

Ein solches Integral ist das Lebesgue-Integral, das die folgende Tatsache ausnutzt, um die Klasse der integrierbaren Funktionen zu vergrößern: Wenn die Werte einer Funktion über die Domäne neu angeordnet werden, sollte das Integral einer Funktion gleich bleiben. So führte Henri Lebesgue das Integral mit seinem Namen ein und erklärte dieses Integral in einem Brief an Paul Montel:^[24]

Ich muss einen bestimmten Betrag bezahlen, den ich in meiner Tasche gesammelt habe. Ich nehme die Scheine und Münzen aus meiner Tasche und gebe sie dem Gläubiger in der Reihenfolge, in der ich sie finde, bis ich die Gesamtsumme erreicht habe. Dies ist das Riemannsche Integral. Aber ich kann anders vorgehen. Nachdem ich das ganze Geld aus meiner Tasche gezogen habe, bestelle ich die Scheine und Münzen nach identischen Werten und zahle dann die mehreren Haufen nacheinander an den Gläubiger. Das ist mein Integral.

Wie Folland es ausdrückt, “Berechnung des Riemannschen Integrals von f, partitioniert man die Domain [a, b] in Teilintervalle”, während im Lebesgue-Integral, “Einer ist in der Tat die Aufteilung des Bereichs von f “.^[25] Die Definition des Lebesgue-Integrals beginnt also mit einem Maß μ. Im einfachsten Fall die Lebesgue-Maßnahme μ((EIN) eines Intervalls EIN = [a, b] ist seine Breite, b – – ein, so dass das Lebesgue-Integral mit dem (richtigen) Riemann-Integral übereinstimmt, wenn beide existieren.^[26] In komplizierteren Fällen können die gemessenen Mengen stark fragmentiert sein, ohne Kontinuität und ohne Ähnlichkeit mit Intervallen.

Verwendung der “Partitionierung des Bereichs von f ” Philosophie, das Integral einer nicht negativen Funktion f :: R. → R. sollte die Summe vorbei sein t der Bereiche zwischen einem dünnen horizontalen Streifen zwischen y = t und y = t + dt. Dieser Bereich ist gerecht μ{ x :: f((x)> t}}dt. Lassen f^∗(( t) = μ{ x ::f(( x)>t}. Das Lebesgue-Integral von f wird dann definiert durch

ist Lebesgue-integrierbar, wenn die Summe der Absolutwerte der Flächen der Regionen zwischen dem Graphen von f und die x-Achse ist endlich:^[28]

${ displaystyle int _ {E} | f | , d mu <+ infty.}$

In diesem Fall ist das Integral wie im Riemannschen Fall die Differenz zwischen der Fläche über dem x-Achse und der Bereich unter dem x-Achse:^[29]

${ displaystyle int _ {E} f , d mu = int _ {E} f ^ {+} , d mu – int _ {E} f ^ {-} , d mu}$

wo

${ displaystyle { begin {alignat} {3} & f ^ {+} (x) && {} = {} max {f (x), 0 } && {} = {} { begin {case} f (x), & { text {if}} f (x)> 0, \ 0, & { text {andernfalls}} end {case}} \ & f ^ {-} (x) && {} = {} max {- f (x), 0 } && {} = {} { begin {case} -f (x), & { text {if}} f (x) <0 , \ 0, & { text {sonst.}} End {Fälle}} end {alignat}}}$

Andere Integrale[edit]

Obwohl die Riemann- und Lebesgue-Integrale die am häufigsten verwendeten Definitionen des Integrals sind, gibt es eine Reihe anderer, darunter:

• Das Darboux-Integral, das durch Darboux-Summen (eingeschränkte Riemann-Summen) definiert ist, entspricht jedoch dem Riemann-Integral – eine Funktion ist genau dann Darboux-integrierbar, wenn sie Riemann-integrierbar ist. Darboux-Integrale haben den Vorteil, dass sie einfacher zu definieren sind als Riemann-Integrale.
• Das Riemann-Stieltjes-Integral, eine Erweiterung des Riemann-Integrals, die sich in Bezug auf eine Funktion im Gegensatz zu einer Variablen integriert.
• Das von Johann Radon weiterentwickelte Lebesgue-Stieltjes-Integral, das sowohl das Riemann-Stieltjes- als auch das Lebesgue-Integral verallgemeinert.
• Das Daniell-Integral, das das Lebesgue-Integral und das Lebesgue-Stieltjes-Integral ohne Abhängigkeit von Maßnahmen zusammenfasst.
• Das Haar-Integral, das 1933 von Alfréd Haar für die Integration in lokal kompakte topologische Gruppen verwendet wurde.
• Das Henstock-Kurzweil-Integral, das von Arnaud Denjoy, Oskar Perron und (am elegantesten als Eichintegral) Jaroslav Kurzweil unterschiedlich definiert und von Ralph Henstock entwickelt wurde.
• Das Itô-Integral und das Stratonovich-Integral, die die Integration in Bezug auf Semimartingale wie die Brownsche Bewegung definieren.
• Das Young-Integral, eine Art Riemann-Stieltjes-Integral in Bezug auf bestimmte Funktionen unbegrenzter Variation.
• Das grobe Pfadintegral, das für Funktionen definiert ist, die mit einigen zusätzlichen Funktionen ausgestattet sind “rauer Weg” strukturiert und verallgemeinert die stochastische Integration sowohl gegen Semimartingale als auch gegen Prozesse wie die fraktionierte Brownsche Bewegung.
• Das Choquet-Integral, ein subadditives oder superadditives Integral, das 1953 vom französischen Mathematiker Gustave Choquet erstellt wurde.

Eigenschaften[edit]

Linearität[edit]

Die Sammlung von Riemann-integrierbaren Funktionen in einem geschlossenen Intervall [a, b] bildet einen Vektorraum unter den Operationen der punktweisen Addition und Multiplikation mit einem Skalar und der Operation der Integration

${ displaystyle f mapsto int _ {a} ^ {b} f (x) ; dx}$

ist eine lineare Funktion in diesem Vektorraum. Somit wird die Sammlung integrierbarer Funktionen unter linearen Kombinationen geschlossen, und das Integral einer linearen Kombination ist die lineare Kombination der Integrale:^[30]

${ displaystyle int _ {a} ^ {b} ( alpha f + beta g) (x) , dx = alpha int _ {a} ^ {b} f (x) , dx + beta int _ {a} ^ {b} g (x) , dx. ,}$

In ähnlicher Weise die Menge der realwertigen Lebesgue-integrierbaren Funktionen auf einem gegebenen Messraum E. mit Maß μ wird unter linearen Kombinationen geschlossen und bildet somit einen Vektorraum und das Lebesgue-Integral

${ displaystyle f mapsto int _ {E} f , d mu}$

ist eine lineare Funktion in diesem Vektorraum, so dass:^[29]

${ displaystyle int _ {E} ( alpha f + beta g) , d mu = alpha int _ {E} f , d mu + beta int _ {E} g , d mu.}$

Betrachten Sie allgemein den Vektorraum aller messbaren Funktionen in einem Messraum ((E., μ)Nehmen von Werten in einem lokal kompakten vollständigen topologischen Vektorraum V. über ein lokal kompaktes topologisches Feld K., f :: E. → V.. Dann kann man eine abstrakte Integrationskarte definieren, die jeder Funktion zugewiesen wird f ein Element von V. oder das Symbol ∞,

${ displaystyle f mapsto int _ {E} f , d mu, ,}$

das ist kompatibel mit linearen Kombinationen.^[31] In dieser Situation gilt die Linearität für den Unterraum von Funktionen, deren Integral ein Element von ist V. (dh “endlich”). Die wichtigsten Sonderfälle treten auf, wenn K. ist R., C.oder eine endliche Erweiterung des Feldes Q._p von p-adischen Zahlen und V. ist ein endlichdimensionaler Vektorraum über K., und wann K. = C. und V. ist ein komplexer Hilbert-Raum.

Linearität, zusammen mit einigen natürlichen Kontinuitätseigenschaften und Normalisierung für eine bestimmte Klasse von “einfach” Funktionen können verwendet werden, um eine alternative Definition des Integrals zu geben. Dies ist der Ansatz von Daniell für den Fall von reellen Funktionen an einer Menge X., verallgemeinert von Nicolas Bourbaki auf Funktionen mit Werten in einem lokal kompakten topologischen Vektorraum. Siehe Hildebrandt 1953 für eine axiomatische Charakterisierung des Integrals.

Ungleichungen[edit]

Eine Reihe allgemeiner Ungleichungen gilt für Riemann-integrierbare Funktionen, die in einem geschlossenen und begrenzten Intervall definiert sind [a, b] und kann auf andere Begriffe des Integrals verallgemeinert werden (Lebesgue und Daniell).

• Ober- und Untergrenze. Eine integrierbare Funktion f auf [a, b]ist notwendigerweise auf dieses Intervall begrenzt. Es gibt also reelle Zahlen m und M. damit m ≤f(( x) ≤M. für alle x im [a, b]. Da die unteren und oberen Summen von f Über [a, b] sind daher jeweils begrenzt durch m (( b– –ein) und M. (( b– –ein), es folgt dem

${ displaystyle m (ba) leq int _ {a} ^ {b} f (x) , dx leq M (ba).}$

• Ungleichungen zwischen Funktionen.^[32] Wenn f(( x) ≤G((x) für jeden x im [a, b] dann jeweils die oberen und unteren Summen von f ist oben durch die oberen bzw. unteren Summen von begrenzt G. So

${ displaystyle int _ {a} ^ {b} f (x) , dx leq int _ {a} ^ {b} g (x) , dx.}$

Dies ist eine Verallgemeinerung der obigen Ungleichungen, wie M. (( b– –ein) ist das Integral der konstanten Funktion mit Wert M. Über [a, b].

Wenn außerdem die Ungleichung zwischen Funktionen streng ist, ist auch die Ungleichung zwischen Integralen streng. Das heißt, wenn f(( x)G((x ) für jeden x im [a, b], dann

${ displaystyle int _ {a} ^ {b} f (x) , dx < int _ {a} ^ {b} g (x) , dx.}$

• Teilintervalle.Wenn [c, d] ist ein Subintervall von [a, b] und f(( x) ist nicht negativ für alle x, dann

${ displaystyle int _ {c} ^ {d} f (x) , dx leq int _ {a} ^ {b} f (x) , dx.}$

${ Anzeigestil (fg) (x) = f (x) g (x), ; f ^ {2} (x) = (f (x)) ^ {2}, ; | f | (x) = | f (x) |. ,}$

Wenn f ist Riemann-integrierbar auf [a, b] dann gilt das gleiche für |f|, und

${ displaystyle left | int _ {a} ^ {b} f (x) , dx right | leq int _ {a} ^ {b} | f (x) | , dx.}$

Darüber hinaus, wenn f und G sind dann beide Riemann-integrierbar fg ist auch Riemann-integrierbar, und

${ displaystyle left ( int _ {a} ^ {b} (fg) (x) , dx right) ^ {2} leq left ( int _ {a} ^ {b} f (x) ) ^ {2} , dx right) left ( int _ {a} ^ {b} g (x) ^ {2} , dx right).}$

Diese als Cauchy-Schwarz-Ungleichung bekannte Ungleichung spielt eine herausragende Rolle in der Hilbert-Raumtheorie, in der die linke Seite als inneres Produkt zweier quadratintegrierbarer Funktionen interpretiert wird f und G auf das Intervall [a, b].

• Hölders Ungleichung.^[33] Nehme an, dass p und q sind zwei reelle Zahlen, 1 ≤ p , q≤ ∞ mit 1/.p + 1/.q = 1, und f und G sind zwei Riemann-integrierbare Funktionen. Dann die Funktionen |f|^p und |G|^q sind auch integrierbar und die folgende Hölder-Ungleichung gilt:

${ displaystyle left | int f (x) g (x) , dx right | leq left ( int left | f (x) right | ^ {p} , dx right) ^ {1 / p} left ( int left | g (x) right | ^ {q} , dx right) ^ {1 / q}.}$

Zum p = q = 2, Hölders Ungleichung wird zur Cauchy-Schwarz-Ungleichung.

• Minkowski-Ungleichung .^[33] Nehme an, dass p ≥ 1 ist eine reelle Zahl und f und G sind Riemann-integrierbare Funktionen. Dann | f |^p, | G |^p und | f + G |^p sind auch Riemann-integrierbar und die folgende Minkowski-Ungleichung gilt:

${ displaystyle left ( int left | f (x) + g (x) right | ^ {p} , dx right) ^ {1 / p} leq left ( int left | f (x) rechts | ^ {p} , dx rechts) ^ {1 / p} + links ( int links | g (x) rechts | ^ {p} , dx rechts) ^ { 1 / p}.}$

Ein Analogon dieser Ungleichung für das Lebesgue-Integral wird bei der Konstruktion von L verwendet^p Räume.

Konventionen[edit]

In diesem Abschnitt, f ist eine realwertige Riemann-integrierbare Funktion. Das Integral

${ displaystyle int _ {a} ^ {b} f (x) , dx}$

über ein Intervall [a, b] ist definiert wenn ein < b. Dies bedeutet, dass die oberen und unteren Summen der Funktion f werden auf einer Partition ausgewertet ein = x₀ ≤ x₁ ≤. . . ≤ x_n = b deren Werte x_ich sind steigend. Geometrisch bedeutet dies, dass die Integration stattfindet “links nach rechts”, auswerten f innerhalb von Intervallen [x_i , x_i +1] wobei ein Intervall mit einem höheren Index rechts von einem Intervall mit einem niedrigeren Index liegt. Die Werte ein und bDie Endpunkte des Intervalls werden als Integrationsgrenzen von bezeichnet f. Integrale können auch definiert werden, wenn ein > b::^[18]

${ displaystyle int _ {a} ^ {b} f (x) , dx = – int _ {b} ^ {a} f (x) , dx.}$

Mit ein = bbedeutet dies:

${ displaystyle int _ {a} ^ {a} f (x) , dx = 0.}$

Die erste Konvention ist notwendig, um Integrale über Teilintervalle von zu übernehmen [a, b];; Das zweite besagt, dass ein Integral, das über ein entartetes Intervall oder einen Punkt genommen wird, Null sein sollte. Ein Grund für die erste Konvention ist die Integrierbarkeit von f in einem Intervall [a, b] impliziert, dass f ist in jedem Subintervall integrierbar [c, d], aber insbesondere Integrale haben die Eigenschaft, dass wenn c ist ein beliebiges Element von [a, b], dann:^[30]

${ displaystyle int _ {a} ^ {b} f (x) , dx = int _ {a} ^ {c} f (x) , dx + int _ {c} ^ {b} f ( x) , dx.}$

Mit der ersten Konvention ergibt sich die Beziehung

${ displaystyle { begin {align} int _ {a} ^ {c} f (x) , dx & {} = int _ {a} ^ {b} f (x) , dx- int _ {c} ^ {b} f (x) , dx \ & {} = int _ {a} ^ {b} f (x) , dx + int _ {b} ^ {c} f (x ) , dx end {align}}}$

ist dann für jede zyklische Permutation von gut definiert ein, b, und c.

Grundsatz der Analysis[edit]

Das Grundsatz der Analysisist die Aussage, dass Differenzierung und Integration inverse Operationen sind: Wenn eine kontinuierliche Funktion zuerst integriert und dann differenziert wird, wird die ursprüngliche Funktion abgerufen.^[34] Eine wichtige Konsequenz, manchmal auch alszweiter grundlegender Satz der Analysisermöglicht die Berechnung von Integralen unter Verwendung eines Antiderivativs der zu integrierenden Funktion.^[35]

Erster Satz[edit]

Lassen f eine kontinuierliche reelle Funktion sein, die in einem geschlossenen Intervall definiert ist [a, b]. Lassen F. sei die definierte Funktion für alle x im [a, b], durch

${ displaystyle F ‘(x) = f (x)}$

für alle x im (( ein,b).

Zweiter Satz[edit]

Lassen f eine reelle Funktion sein, die in einem geschlossenen Intervall definiert ist [a, b] das lässt ein Antiderivativ zu F. auf [a, b]. Das ist, f und F. sind Funktionen, die für alle x im [a, b],

${ displaystyle f (x) = F ‘(x).}$

Wenn f ist auf integrierbar [a, b] dann

${ displaystyle int _ {a} ^ {b} f (x) , dx = F (b) -F (a).}$

Erweiterungen[edit]

Unsachgemäße Integrale[edit]

Das falsche Integral

${ displaystyle int _ {0} ^ { infty} { frac {dx} {(x + 1) { sqrt {x}}} = pi}$

hat unbegrenzte Intervalle für Domäne und Bereich.

EIN “richtig” Das Riemannsche Integral geht davon aus, dass der Integrand in einem geschlossenen und begrenzten Intervall definiert und endlich ist, geklammert durch die Integrationsgrenzen. Ein falsches Integral tritt auf, wenn eine oder mehrere dieser Bedingungen nicht erfüllt sind. In einigen Fällen können solche Integrale definiert werden, indem die Grenze einer Folge geeigneter Riemann-Integrale in zunehmend größeren Intervallen berücksichtigt wird.

Wenn das Intervall unbegrenzt ist, beispielsweise an seinem oberen Ende, ist das falsche Integral die Grenze, wenn dieser Endpunkt gegen unendlich geht:^[36]

${ displaystyle int _ {a} ^ { infty} f (x) , dx = lim _ {b bis infty} int _ {a} ^ {b} f (x) , dx. }}$

Wenn der Integrand beispielsweise nur in einem halboffenen Intervall definiert oder endlich ist (( ein, b]]Andererseits kann eine Grenze ein endliches Ergebnis liefern:^[37]

${ displaystyle int _ {a} ^ {b} f (x) , dx = lim _ { varepsilon bis 0} int _ {a + epsilon} ^ {b} f (x) , dx .}$

Das heißt, das falsche Integral ist die Grenze der richtigen Integrale, wenn sich ein Endpunkt des Integrationsintervalls entweder einer bestimmten reellen Zahl oder nähert ∞, oder −∞. In komplizierteren Fällen sind Grenzwerte an beiden Endpunkten oder an inneren Punkten erforderlich.

Mehrfachintegration[edit]

Das doppelte Integral berechnet das Volumen unter einer Oberfläche

${ displaystyle z = f (x, y)}$

Ebenso wie das bestimmte Integral einer positiven Funktion einer Variablen die Fläche des Bereichs zwischen dem Graphen der Funktion und dem darstellt x -Achse, die Doppelintegral einer positiven Funktion zweier Variablen repräsentiert das Volumen des Bereichs zwischen der durch die Funktion definierten Oberfläche und der Ebene, die ihre Domäne enthält.^[38] Beispielsweise hängt eine Funktion in zwei Dimensionen von zwei reellen Variablen ab: xund y und das Integral einer Funktion f über dem Rechteck R. angegeben als kartesisches Produkt zweier Intervalle

${ displaystyle R =[a,b]mal [c,d]}}$

kann geschrieben werden

${ displaystyle int _ {R} f (x, y) , dA}$

wo das Differential dA gibt an, dass die Integration in Bezug auf die Fläche erfolgt. Dieses Doppelintegral kann mit Riemannschen Summen definiert werden und repräsentiert das (vorzeichenbehaftete) Volumen unter dem Diagramm von z=f((x, y) über die Domain R. .^[39] Unter geeigneten Bedingungen (z. B. wenn f ist stetig), besagt der Satz von Fubini, dass dieses Integral als äquivalentes iteriertes Integral ausgedrückt werden kann^[40]

${ displaystyle int _ {a} ^ {b} left[int _{c}^{d}f(x,y),dyright], dx.}$

Dies reduziert das Problem der Berechnung eines Doppelintegrals auf die Berechnung eindimensionaler Integrale. Aus diesem Grund eine andere Notation für das Integral über R.verwendet ein doppeltes Integralzeichen:^[39]

${ displaystyle iint _ {R} f (x, y) , dA.}$

Die Integration über allgemeinere Domänen ist möglich. Das Integral einer Funktion fin Bezug auf das Volumen über ein n- dimensionale Region D. von

${ displaystyle mathbb {R} ^ {n}}$

wird durch Symbole wie:

${ displaystyle int _ {D} f ( mathbf {x}) d ^ {n} mathbf {x} = int _ {D} f , dV.}$

Linienintegrale und Oberflächenintegrale[edit]

Ein Linienintegral summiert Elemente entlang einer Kurve.

Das Konzept eines Integrals kann auf allgemeinere Integrationsbereiche wie gekrümmte Linien und Flächen in höherdimensionalen Räumen ausgedehnt werden. Solche Integrale sind als Linienintegrale bzw. Oberflächenintegrale bekannt. Diese haben wichtige Anwendungen in der Physik, beispielsweise beim Umgang mit Vektorfeldern.

EIN Linienintegral(manchmal a genannt Pfadintegral) ist ein Integral, bei dem die zu integrierende Funktion entlang einer Kurve ausgewertet wird.^[41] Es werden verschiedene Leitungsintegrale verwendet. Bei einer geschlossenen Kurve wird sie auch als a bezeichnet Konturintegral .

Die zu integrierende Funktion kann ein Skalarfeld oder ein Vektorfeld sein. Der Wert des Linienintegrals ist die Summe der Werte des Feldes an allen Punkten der Kurve, gewichtet mit einer Skalarfunktion auf der Kurve (üblicherweise Bogenlänge oder für ein Vektorfeld das Skalarprodukt des Vektorfeldes mit einem Differential Vektor in der Kurve).^[42] Diese Gewichtung unterscheidet das Linienintegral von einfacheren Integralen, die in Intervallen definiert sind. Viele einfache Formeln in der Physik haben natürliche kontinuierliche Analoga in Bezug auf Linienintegrale; zum Beispiel die Tatsache, dass Arbeit gleich Kraft ist, F.multipliziert mit Verschiebung, skann ausgedrückt werden (in Form von Vektorgrößen) als:^[43]

${ displaystyle W = mathbf {F} cdot mathbf {s}.}$

Für ein Objekt, das sich entlang eines Pfades bewegt C. in einem Vektorfeld F. B. ein elektrisches Feld oder ein Gravitationsfeld, wird die Gesamtarbeit, die das Feld auf dem Objekt leistet, durch Summieren der Differentialarbeit erhalten, die beim Bewegen von ausgeführt wird s zu s + ds. Dies ergibt das Linienintegral^[44]

${ displaystyle W = int _ {C} mathbf {F} cdot d mathbf {s}.}$

Die Definition des Oberflächenintegrals beruht auf der Aufteilung der Oberfläche in kleine Oberflächenelemente.

EINOberflächenintegralverallgemeinert Doppelintegrale auf die Integration über eine Oberfläche (die eine gekrümmte Menge im Raum sein kann); es kann als das Doppelintegralanalog des Linienintegrals angesehen werden. Die zu integrierende Funktion kann ein Skalarfeld oder ein Vektorfeld sein. Der Wert des Oberflächenintegrals ist die Summe des Feldes an allen Punkten der Oberfläche. Dies kann erreicht werden, indem die Oberfläche in Oberflächenelemente aufgeteilt wird, die die Aufteilung für Riemann-Summen ermöglichen.^[45]

Betrachten Sie als Beispiel für Anwendungen von Oberflächenintegralen ein Vektorfeld v auf einer Oberfläche S.;; das heißt, für jeden Punkt x im S., v((x) ist ein Vektor. Stellen Sie sich vor, eine Flüssigkeit fließt durch S., so dass v(( x) bestimmt die Geschwindigkeit der Flüssigkeit bei x. Der Fluss ist definiert als die Menge der durchfließenden Flüssigkeit S. in Zeiteinheiten. Um das Flussmittel zu finden, muss man das Punktprodukt von nehmen v mit der Einheitsoberfläche normal zu S. an jedem Punkt, der ein Skalarfeld ergibt, das über die Oberfläche integriert ist:^[46]

${ displaystyle int _ {S} { mathbf {v}} cdot , d { mathbf {S}}.}$

Der Fluidfluss in diesem Beispiel kann von einem physikalischen Fluid wie Wasser oder Luft oder von einem elektrischen oder magnetischen Fluss stammen. Somit haben Oberflächenintegrale Anwendungen in der Physik, insbesondere mit der klassischen Theorie des Elektromagnetismus.

Konturintegrale[edit]

In der komplexen Analyse ist der Integrand eine komplexwertige Funktion einer komplexen Variablen z anstelle einer reellen Funktion einer reellen Variablen x. Wenn eine komplexe Funktion entlang einer Kurve integriert ist

${ displaystyle gamma}$

in der komplexen Ebene wird das Integral wie folgt bezeichnet

${ displaystyle int _ { gamma} f (z) , dz.}$

Dies ist als Konturintegral bekannt.

Integrale differentieller Formen[edit]

Eine Differentialform ist ein mathematisches Konzept in den Bereichen multivariabler Kalkül, Differentialtopologie und Tensoren. Differentialformen sind graduell organisiert. Zum Beispiel ist eine Einform eine gewichtete Summe der Differentiale der Koordinaten, wie zum Beispiel:

${ Anzeigestil E (x, y, z) , dx + F (x, y, z) , dy + G (x, y, z) , dz}$

wo E., F. , Gsind Funktionen in drei Dimensionen. Eine differentielle Einform kann über einen orientierten Pfad integriert werden, und das resultierende Integral ist nur eine andere Art, ein Linienintegral zu schreiben. Hier die grundlegenden Unterschiede dx, dy ,dzMessen Sie infinitesimal ausgerichtete Längen parallel zu den drei Koordinatenachsen.

Eine differentielle Zwei-Form ist eine Summe der Form

${ Anzeigestil G (x, y, z) , dx Keil dy + E (x, y, z) , dy Keil dz + F (x, y, z) , dz Keil dx.}$

Hier die grundlegenden zwei Formen

${ displaystyle dx wedge dy, dz wedge dx, dy wedge dz}$

Messen Sie orientierte Bereiche parallel zu den Koordinaten-Zwei-Ebenen. Das Symbol

${ displaystyle wedge}$

bezeichnet das Keilprodukt, das dem Kreuzprodukt in dem Sinne ähnlich ist, dass das Keilprodukt zweier Formen, die orientierte Längen darstellen, einen orientierten Bereich darstellt. Eine Zwei-Form kann über eine orientierte Oberfläche integriert werden, und das resultierende Integral entspricht dem Oberflächenintegral, das den Fluss von ergibt

${ displaystyle E mathbf {i} + F mathbf {j} + G mathbf {k}}$

.

Im Gegensatz zum Kreuzprodukt und zur dreidimensionalen Vektorrechnung sind das Keilprodukt und die Berechnung der Differentialformen in beliebiger Dimension und auf allgemeineren Mannigfaltigkeiten (Kurven, Flächen und deren höherdimensionale Analoga) sinnvoll. Die äußere Ableitung spielt die Rolle des Gradienten und der Krümmung der Vektorrechnung, und der Satz von Stokes verallgemeinert gleichzeitig die drei Sätze der Vektorrechnung: den Divergenzsatz, den Satz von Green und den Satz von Kelvin-Stokes.

Zusammenfassungen[edit]

Das diskrete Äquivalent der Integration ist die Summation. Summationen und Integrale können unter Verwendung der Theorie der Lebesgue-Integrale oder der Zeitskalenrechnung auf die gleichen Grundlagen gestellt werden.

Anwendungen[edit]

Integrale werden in vielen Bereichen häufig verwendet. Beispielsweise werden in der Wahrscheinlichkeitstheorie Integrale verwendet, um die Wahrscheinlichkeit zu bestimmen, dass eine Zufallsvariable in einen bestimmten Bereich fällt.^[47] Darüber hinaus muss das Integral unter einer gesamten Wahrscheinlichkeitsdichtefunktion gleich 1 sein, was einen Test liefert, ob eine Funktion ohne negative Werte eine Dichtefunktion sein könnte oder nicht.^[48]

Integrale können zum Berechnen der Fläche eines zweidimensionalen Bereichs mit einer gekrümmten Grenze sowie zum Berechnen des Volumens eines dreidimensionalen Objekts mit einer gekrümmten Grenze verwendet werden. Die Fläche eines zweidimensionalen Bereichs kann unter Verwendung des oben erwähnten bestimmten Integrals berechnet werden.^[49] Das Volumen eines dreidimensionalen Objekts wie einer Scheibe oder Unterlegscheibe kann durch Scheibenintegration unter Verwendung der Gleichung für das Volumen eines Zylinders berechnet werden.

${ displaystyle pi r ^ {2} h}$

, wo

${ displaystyle r}$

ist der Radius. Im Fall einer einfachen Scheibe, die durch Drehen einer Kurve um die erstellt wurde x-Achse, der Radius ist gegeben durch f((x)und seine Höhe ist das Differential dx. Verwenden eines Integrals mit Grenzen ein und bist das Volumen der Disc gleich:^[50]

$${ displaystyle pi int _ {a} ^ {b} f ^ {2} (x) , dx.}$$

Integrale werden auch in der Physik verwendet, in Bereichen wie der Kinematik, um Größen wie Verschiebung, Zeit und Geschwindigkeit zu ermitteln. Zum Beispiel bei geradliniger Bewegung die Verschiebung eines Objekts über das Zeitintervall

${ displaystyle [a,b]}}$

ist gegeben durch:

${ displaystyle W_ {A rightarrow B} = int _ {A} ^ {B} F (x) , dx.}$

Integrale werden auch in der Thermodynamik verwendet, wo die thermodynamische Integration verwendet wird, um die Differenz der freien Energie zwischen zwei gegebenen Zuständen zu berechnen.

Berechnung[edit]

Analytisch[edit]

Die grundlegendste Technik zur Berechnung bestimmter Integrale einer reellen Variablen basiert auf dem Grundsatz der Analysis. Lassen f(( x) sei die Funktion von x über ein bestimmtes Intervall integriert werden [a, b]. Dann finden Sie ein Antiderivativ von f;; das heißt, eine Funktion F. so dass F.‘= f auf das Intervall. Vorausgesetzt, der Integrand und das Integral haben keine Singularitäten auf dem Weg der Integration, nach dem Grundsatz der Analysis,

${ displaystyle int _ {a} ^ {b} f (x) , dx = F (b) -F (a).}$

Manchmal ist es notwendig, eine der vielen Techniken zu verwenden, die zur Bewertung von Integralen entwickelt wurden. Die meisten dieser Techniken schreiben ein Integral als ein anderes um, das hoffentlich leichter zu handhaben ist. Zu den Techniken gehören die Integration durch Substitution, die Integration durch Teile, die Integration durch trigonometrische Substitution und die Integration durch Teilfraktionen.

Es gibt alternative Methoden, um komplexere Integrale zu berechnen. Viele nichtelementare Integrale können in einer Taylor-Reihe erweitert und termweise integriert werden. Gelegentlich können die resultierenden unendlichen Reihen analytisch summiert werden. Die Faltungsmethode unter Verwendung von Meijer-G-Funktionen kann ebenfalls verwendet werden, vorausgesetzt, der Integrand kann als Produkt von Meijer-G-Funktionen geschrieben werden. Es gibt auch viele weniger gebräuchliche Methoden zur Berechnung bestimmter Integrale. Zum Beispiel kann die Identität von Parseval verwendet werden, um ein Integral über einem rechteckigen Bereich in eine unendliche Summe umzuwandeln. Gelegentlich kann ein Integral durch einen Trick bewertet werden. Ein Beispiel hierfür finden Sie unter Gaußsches Integral.

Berechnungen von Volumina von Rotationskörpern können normalerweise mit Plattenintegration oder Shell-Integration durchgeführt werden.

Spezifische Ergebnisse, die mit verschiedenen Techniken erarbeitet wurden, sind in der Liste der Integrale zusammengefasst.

Symbolisch[edit]

Viele Probleme in Mathematik, Physik und Ingenieurwesen betreffen die Integration, bei der eine explizite Formel für das Integral gewünscht wird. Zu diesem Zweck wurden im Laufe der Jahre umfangreiche Integraltabellen erstellt und veröffentlicht. Mit der Verbreitung von Computern haben sich viele Fachleute, Pädagogen und Studenten Computeralgebra-Systemen zugewandt, die speziell für schwierige oder langwierige Aufgaben, einschließlich Integration, entwickelt wurden. Die symbolische Integration war eine der Motivationen für die Entwicklung der ersten derartigen Systeme wie Macsyma und Maple.

Eine große mathematische Schwierigkeit bei der symbolischen Integration besteht darin, dass eine relativ einfache Funktion in vielen Fällen keine Integrale aufweist, die in geschlossener Form ausgedrückt werden können und nur Elementarfunktionen umfassen, einschließlich rationaler und exponentieller Funktionen, Logarithmus, trigonometrischer Funktionen und inverser trigonometrischer Funktionen Operationen der Multiplikation und Zusammensetzung. Der Risch-Algorithmus liefert ein allgemeines Kriterium, um zu bestimmen, ob das Antiderivativ einer Elementarfunktion elementar ist, und um es zu berechnen, wenn dies der Fall ist. Funktionen mit geschlossenen Ausdrücken von Antiderivativen sind jedoch die Ausnahme, und folglich haben computergestützte Algebra-Systeme keine Hoffnung, ein Antiderivativ für eine zufällig konstruierte Elementarfunktion finden zu können. Positiv zu vermerken ist, dass, wenn die “Bausteine” für Antiderivative im Voraus festgelegt werden, möglicherweise noch entschieden werden kann, ob das Antiderivativ einer bestimmten Funktion unter Verwendung dieser Blöcke und Multiplikations- und Kompositionsoperationen ausgedrückt werden kann, und das Symbol gefunden wird antworte wann immer es existiert. Der Risch-Algorithmus, der in Mathematica, Maple und anderen Computeralgebra-Systemen implementiert ist, macht genau das für Funktionen und Antiderivative, die aus rationalen Funktionen, Radikalen, Logarithmus und Exponentialfunktionen aufgebaut sind.

Einige spezielle Integranden treten häufig genug auf, um eine spezielle Untersuchung zu rechtfertigen. Insbesondere kann es nützlich sein, in der Reihe der Antiderivate die speziellen Funktionen zu haben (wie die Legendre-Funktionen, die hypergeometrische Funktion, die Gammafunktion, die unvollständige Gammafunktion usw.). Die Erweiterung des Risch-Algorithmus um solche Funktionen ist möglich, aber herausfordernd und war ein aktives Forschungsthema.

In jüngerer Zeit ist ein neuer Ansatz entstanden, der verwendet D.-finite Funktionen, die Lösungen linearer Differentialgleichungen mit Polynomkoeffizienten sind. Die meisten elementaren und speziellen Funktionen sind D.-finite und das Integral von a D.-finite Funktion ist auch a D.-finite Funktion. Dies liefert einen Algorithmus, um das Antiderivativ von a auszudrücken D.-finite Funktion als Lösung einer Differentialgleichung. Diese Theorie erlaubt es auch, das bestimmte Integral von a zu berechnenD.-Funktion als die Summe einer Reihe, die durch die ersten Koeffizienten gegeben ist, und liefert einen Algorithmus zum Berechnen eines beliebigen Koeffizienten.

Numerisch[edit]

Numerische Quadraturmethoden: Rechteckmethode, Trapezregel, Rombergsche Methode, Gaußsche Quadratur

Bestimmte Integrale können unter Verwendung verschiedener Methoden der numerischen Integration angenähert werden. Die Rechteckmethode beruht auf der Aufteilung des Bereichs unter der Funktion in eine Reihe von Rechtecken, die Funktionswerten entsprechen, und multipliziert mit der Schrittweite, um die Summe zu ermitteln. Ein besserer Ansatz, die Trapezregel, ersetzt die in einer Riemannschen Summe verwendeten Rechtecke durch Trapezoide. Die Trapezregel gewichtet den ersten und den letzten Wert um die Hälfte und multipliziert ihn dann mit der Schrittweite, um eine bessere Annäherung zu erhalten.^[53] Die Idee hinter der Trapezregel, dass genauere Approximationen an die Funktion bessere Approximationen an das Integral ergeben, kann weitergeführt werden: Die Simpson-Regel approximiert den Integranden durch eine stückweise quadratische Funktion.^[54]

Riemannsche Summen, die Trapezregel und die Simpsonsche Regel sind Beispiele für eine Familie von Quadraturregeln, die als Newton-Cotes-Formeln bezeichnet werden. Das Grad n Die Newton-Cotes-Quadraturregel approximiert das Polynom in jedem Subintervall um einen Grad n Polynom. Dieses Polynom wird gewählt, um die Werte der Funktion im Intervall zu interpolieren.^[55] Newton-Cotes-Näherungen mit höherem Grad können genauer sein, erfordern jedoch mehr Funktionsbewertungen und können aufgrund des Runge-Phänomens unter numerischer Ungenauigkeit leiden. Eine Lösung für dieses Problem ist die Clenshaw-Curtis-Quadratur, bei der der Integrand durch Erweiterung auf Chebyshev-Polynome angenähert wird.

Rombergs Methode halbiert die Schrittbreiten schrittweise und ergibt trapezförmige Näherungen, die mit bezeichnet sind T.((h₀), T.((h₁)und so weiter, wo h_k+1 ist die Hälfte von h_k. Für jede neue Schrittgröße muss nur die Hälfte der neuen Funktionswerte berechnet werden. die anderen übertragen von der vorherigen Größe. Es interpoliert dann ein Polynom durch die Näherungen und extrapoliert auf T. (0). Die Gaußsche Quadratur bewertet die Funktion an den Wurzeln eines Satzes orthogonaler Polynome.^[56] Ein nDie Punkt-Gauß-Methode ist genau für Polynome vom Grad bis 2 n – 1.

Bei der Berechnung höherdimensionaler Integrale (z. B. Volumenberechnungen) werden häufig Alternativen wie die Monte-Carlo-Integration verwendet.^[57]

Mechanisch[edit]

Die Fläche einer beliebigen zweidimensionalen Form kann mit einem Messgerät namens Planimeter bestimmt werden. Das Volumen unregelmäßiger Objekte kann durch die beim Eintauchen des Objekts verdrängte Flüssigkeit präzise gemessen werden.

Geometrisch[edit]

Die Fläche kann manchmal über geometrische Kompass- und Linealkonstruktionen eines äquivalenten Quadrats gefunden werden.

Siehe auch[edit]

1. ^ Die in diesem Artikel diskutierte Integralrechnung ist eine sehr gut etablierte mathematische Disziplin, für die es viele Quellen gibt. Siehe zum Beispiel Apostol 1967 und Anton, Bivens & Davis 2016.

Verweise[edit]

1. ^ Burton 2011, p. 117.
2. ^ Heath 2002.
3. ^ Katz 2009, S. 201–204.
4. ^ Katz 2009, S. 284–285.
5. ^ Katz 2009, S. 305–306.
6. ^ Katz 2009, S. 516–517.
7. ^ Struik 1986, S. 215–216.
8. ^ Katz 2009, S. 536–537.
9. ^ Burton 2011, S. 385–386.
10. ^ Stillwell 1989, p. 131.
11. ^ Katz 2009, S. 628–629.
12. ^ Katz 2009, p. 785.
13. ^ Burton 2011, p. 414; Leibniz 1899, p. 154.
14. ^ Cajori 1929, S. 249–250; Fourier 1822, §231.
15. ^ Cajori 1929, p. 246.
16. ^ Cajori 1929, p. 182.
17. ^ W3C 2006.
18. ^ ^{ein b} Apostol 1967, p. 74.
19. ^ Anton, Bivens & Davis 2016, p. 259.
20. ^ Apostol 1967, p. 69.
21. ^ Anton, Bivens & Davis 2016, S. 286–287.
22. ^ Krantz 1991, p. 173.
23. ^ Rudin 1987, p. 5.
24. ^ Siegmund-Schultze 2008, p. 796.
25. ^ Folland 1999, S. 57–58.
26. ^ Bourbaki 2004, p. IV.43.
27. ^ Lieb & Loss 2001, p. 14.
28. ^ Folland 1999, p. 53.
29. ^ ^{ein b} Rudin 1987, p. 25.
30. ^ ^{ein b} Apostol 1967, p. 80.
31. ^ Rudin 1987, p. 54.
32. ^ Apostol 1967, p. 81.
33. ^ ^{ein b} Rudin 1987, p. 63.
34. ^ Apostol 1967, p. 202.
35. ^ Apostol 1967, p. 205.
36. ^ Apostol 1967, p. 416.
37. ^ Apostol 1967, p. 418.
38. ^ Anton, Bivens & Davis 2016, p. 895.
39. ^ ^{ein b} Anton, Bivens & Davis 2016, p. 896.
40. ^ Anton, Bivens & Davis 2016, p. 897.
41. ^ Anton, Bivens & Davis 2016, p. 980.
42. ^ Anton, Bivens & Davis 2016, p. 981.
43. ^ Anton, Bivens & Davis 2016, p. 697.
44. ^ Anton, Bivens & Davis 2016, p. 991.
45. ^ Anton, Bivens & Davis 2016, p. 1014.
46. ^ Anton, Bivens & Davis 2016, p. 1024.
47. ^ Feller 1966, p. 1.
48. ^ Feller 1966, p. 3.
49. ^ Apostol 1967, S. 88–89.
50. ^ Apostol 1967, S. 111–114.
51. ^ Anton, Bivens & Davis 2016, p. 306.
52. ^ Apostol 1967, p. 116.
53. ^ Dahlquist & Björck 2008, S. 519–520.
54. ^ Dahlquist & Björck 2008, S. 522–524.
55. ^ Kahaner, Moler & Nash 1989, p. 144.
56. ^ Kahaner, Moler & Nash 1989, p. 147.
57. ^ Kahaner, Moler & Nash 1989, S. 139–140.

Literaturverzeichnis[edit]

• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016), Kalkül: Frühe Transzendentale(11. Aufl.), John Wiley & Sons, ISBN 978-1-118-88382-2
• Apostol, Tom M. (1967), Calculus, Vol. 1: Einvariablenrechnung mit Einführung in die lineare Algebra (2. Aufl.), Wiley, ISBN 978-0-471-00005-1
• Bourbaki, Nicolas (2004), Integration I. , Springer-Verlag, ISBN 3-540-41129-1. Insbesondere die Kapitel III und IV.
• Burton, David M. (2011), Die Geschichte der Mathematik: Eine Einführung(7. Aufl.), McGraw-Hill, ISBN 978-0-07-338315-6
• Cajori, Florian (1929), Eine Geschichte der mathematischen Notationen Band II, Open Court Publishing, ISBN 978-0-486-67766-8
• Dahlquist, Germund; Björck, Åke (2008), “Kapitel 5: Numerische Integration”, Numerische Methoden im wissenschaftlichen Rechnen, Band I. , Philadelphia: SIAM, archiviert von das Original am 15.06.2007
• Feller, William (1966), Eine Einführung in die Wahrscheinlichkeitstheorie und ihre Anwendungen, John Wiley & Sons
• Folland, Gerald B. (1999), Reale Analyse: Moderne Techniken und ihre Anwendungen(2. Aufl.), John Wiley & Sons, ISBN 0-471-31716-0
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231Verfügbar in Übersetzung als Fourier, Joseph (1878), Die analytische Theorie der WärmeFreeman, Alexander (trans.), Cambridge University Press, S. 200–201
• Heath, TL, hrsg. (2002), Die Werke von Archimedes, Dover, ISBN 978-0-486-42084-4(Ursprünglich veröffentlicht von Cambridge University Press, 1897, basierend auf der griechischen Version von JL Heiberg.)
• Hildebrandt, TH (1953), “Integration in abstrakte Räume”, Bulletin der American Mathematical Society, 59 (2): 111–139, doi:10.1090 / S0002-9904-1953-09694-X, ISSN 0273-0979
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989), “Kapitel 5: Numerische Quadratur”, Numerische Methoden und Software, Prentice Hall, ISBN 978-0-13-627258-8
• Kallio, Bruce Victor (1966), Eine Geschichte des bestimmten Integrals (PDF) (Magisterarbeit), University of British Columbia, archiviert von das Original (PDF) am 05.03.2014abgerufen 28.02.2014
• Katz, Victor J. (2009), Eine Geschichte der Mathematik: Eine Einführung, Addison-Wesley, ISBN 0-321-38700-7
• Krantz, Steven G. (1991), Reale Analyse und Grundlagen, CRC Press, ISBN 0-8493-7156-2
• Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel (Hrsg.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
• Lieb, Elliott; Verlust, Michael (2001), Analyse , Studium der Mathematik, 14 (2. Aufl.), American Mathematical Society, ISBN 978-0821827833
• Rudin, Walter (1987), “Kapitel 1: Abstrakte Integration”, Reale und komplexe Analyse(Internationale Ausgabe), McGraw-Hill, ISBN 978-0-07-100276-9
• Saks, Stanisław (1964), Theorie des Integrals (Englische Übersetzung von LC Young. Mit zwei zusätzlichen Anmerkungen von Stefan Banach. Zweite überarbeitete Ausgabe.), New York: Dover
• Siegmund-Schultze, Reinhard (2008), “Henri Lebesgue”in Timothy Gowers; June Barrow-Green; Imre Leader (Hrsg.), Princeton Begleiter der Mathematik , Princeton University Press, ISBN 978-0-691-11880-2.
• Stillwell, John (1989), Mathematik und ihre Geschichte, Springer, ISBN 0-387-96981-0
• Stoer, Josef; Bulirsch, Roland (2002), “Themen in der Integration”, Einführung in die numerische Analyse(3. Aufl.), Springer, ISBN 978-0-387-95452-3.
• Struik, Dirk Jan, Hrsg. (1986), Ein Quellenbuch in Mathematik, 1200-1800, Princeton, New Jersey: Princeton University Press, ISBN 0-691-08404-1
• W3C (2006), Arabische mathematische Notation

Externe Links[edit]

Wikibooks hat ein Buch zum Thema: Infinitesimalrechnung

Online-Bücher[edit]

• Keisler, H. Jerome, Elementarrechnung: Ein Ansatz mit Infinitesimalen, Universität von Wisconsin
• Stroyan, KD, Eine kurze Einführung in die Infinitesimalrechnung, Universität von Iowa
• Mauch, Sean, Seans Angewandtes Mathematikbuch, CIT, ein Online-Lehrbuch, das eine vollständige Einführung in die Analysis enthält
• Crowell, Benjamin, Infinitesimalrechnung, Fullerton College, ein Online-Lehrbuch
• Garrett, Paul, Anmerkungen zur Berechnung des ersten Jahres
• Hussain, Faraz, Kalkül verstehen, ein Online-Lehrbuch
• Johnson, William Woolsey (1909) Elementare Abhandlung über Integralrechnung, Link von HathiTrust.
• Kowalk, WP, Integrationstheorie, Universität Oldenburg. Ein neues Konzept für ein altes Problem. Online-Lehrbuch
• Sloughter, Dan, Differenzgleichungen zu Differentialgleichungen, eine Einführung in die Analysis
• Numerische Integrationsmethoden beimInstitut für ganzheitliche numerische Methoden
• PS Wang, Bewertung bestimmter Integrale durch symbolische Manipulation (1972) – ein Kochbuch bestimmter integraler Techniken