モデルカテゴリ – ウィキペディア
数学的なホモトピエット理論では1つです モデルカテゴリ 「弱い等価」、「ファイバー」、「コファーゼ」と呼ばれる矢印のサブクラスを選択したカテゴリ。これらのクラスの要件は、対応するトポロジー用語の抽象化を表し、トポロジールームのカテゴリだけでなく、チェーン複合体のカテゴリにも関連するホモトピーカテゴリの構築を可能にします。後者の場合、関連するホモトピーのカテゴリは、廃止されたカテゴリと呼ばれます。
この用語は、1967年にダニエル・G・クレンによって導入されました。
カテゴリで
授与されたカテゴリの下で同じ3つのオブジェクトです。
- 弱い同等性
- ファイバ
- cofasolations。
(CO-)ファイバーを呼び出します 非環式 また 些細な 、それらが同時に弱い同等の場合。
次の公理が満たされている場合、モデルカテゴリを意味します。
MC1((KO-)LIMITES) [ 編集 | ソーステキストを編集します ]
ついにビボルです。
MC2( “3 fron 3″) [ 編集 | ソーステキストを編集します ]
それは
矢印
そのうちの2つは、3番目を含む弱い同等性です。
MC3(Retrakte) [ 編集 | ソーステキストを編集します ]
は
矢印の撤回
それは優れたサブカテゴリの1つに属しているので、属します
同じサブカテゴリの。
MC4(リフティング) [ 編集 | ソーステキストを編集します ]
通勤図にあります
補助、
ファッシングと
また
azyclical、
だから矢印があります
それは図を通勤します。
MC5(分解) [ 編集 | ソーステキストを編集します ]
1.各矢印は次のとおりです
繊維用
そして、azyclicalのクーファウアー
表現されています。
2.各矢印は次のとおりです
azyclical繊維用
そして、クーファイバー
表現されています。
- 定義は自己二重です:デュアルカテゴリ また、ファイバーとクーファイバーのクラスのみが交換されるモデルカテゴリの構造も備えています。
- 公理 MC4 繊維とクーファイバーのクラスを特徴付ける:矢印 は その後、まさに すべての図があるときの魅力 Azyclicの凝固は持ち上げです (それに応じてコファーゼの場合)。したがって、モデルカテゴリ構造は、弱い等価性を指定することにより、すでに 一 明確に定義されている繊維とフーバーのクラスの。
- 繊維のクラスは、コバシスの変化の下で安定している基礎の基礎よりも安定しています。
FaserneおよびCoofiberオブジェクト [ 編集 | ソーステキストを編集します ]
後 MC1 含む
特に初期オブジェクト
そしてエンドオブジェクト
。
オブジェクト
呼ばれています 忠実 、 もしも
魅力はそうです Kofasernd 、 もしも
補助はです。
トポロジールーム [ 編集 | ソーステキストを編集します ]
カテゴリで
通常、次のモデルカテゴリ構造はトポロジールームと見なされます。
弱いホモトピーの等価性は、繊維が選択されているため、弱い同等性として選択されます。
トポロジ室には、弱い同等性がホモトピーの同等性であるモデル構造を提供することもできます。
チェーン錯体 [ 編集 | ソーステキストを編集します ]
カテゴリ
非陰性インデックスを持つR-Modulnの鎖複合体には、次のモデルカテゴリ構造があります。
ホモトピアの概念をモデルカテゴリに転送できるようにするために、シリンダーオブジェクトとパスが定義されています。
その助けを借りて、左および右のホモトピアが定義されています。
これらの2つのホモトープ取引は、一般に同等の比率ではなく、お互いに同意するものでもありません。
検討中の矢のソースと目的地が忠実で繊維状である場合、両方の定義は同じ等価関係を説明しています。
したがって、次のようにホモトピーのカテゴリに変換できます。まず、矢印は、等価性が低いだけでなく、繊維とクーファイバーのソースと目標を持っている人によってフィールドに置き換えられます。次に、左または右翼のホモトパ矢印の同等のクラスをホモトピークラスに要約して、ホモトピーカテゴリを取得できます。
ホモトピーカテゴリへの移行を弱い同等性に関するローカリゼーションとして説明することもできるため、ホモトピーカテゴリの構築のためのファイバーとCOファイバーを知る必要はありません。
- W. G. DwyerとJ. Spalinski: ホモトピー理論とモデルカテゴリ (PDFファイル; 419 KB)、1995
- マーク・ホーヴィー: モデルカテゴリ 、1999、ISBN 0-8218-1359-5
- ダニエル・G・クレン: ホモトピカル代数 、数学の講義ノート、Vol。 43、Springer-Verlag、1967。
- J. P.メイ、J。Sigurdsson: パラメータ化されたホモトピー理論 、2006年 [初め] 、ISBN 0-8218-3922-5
- Ken-ichi Maruyama, John W. Rutter: ホモトピーの自己等価性と関連トピックのグループ 、2001年 [2] 、ISBN 0-8218-2683-2
- すべてのマナルマン、病気、アアレルはミーを与えました、.magas melgram、doublay yanan:euile: ホモトピー理論とその応用 、現代数学、ボリューム:188、アメリカ数学協会、1995年 [3] 、ISBN 0-8218-0305-0。
- サイモン・サラモン、ブライアン・ステア、ウィルソン・アレクサンダー・サザーランド: ホモトピー理論の進歩 、ケンブリッジ大学出版局、1989年 [4] 、ISBN 0-521-37907-5。
 授与されたカテゴリの下で同じ3つのオブジェクトです。
授与されたカテゴリの下で同じ3つのオブジェクトです。  矢印
矢印  矢印の撤回
矢印の撤回  それは優れたサブカテゴリの1つに属しているので、属します
それは優れたサブカテゴリの1つに属しているので、属します 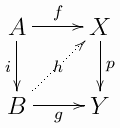
 補助、
補助、  ファッシングと
ファッシングと  それは図を通勤します。
それは図を通勤します。  繊維用
繊維用 

 そしてエンドオブジェクト
そしてエンドオブジェクト  。
。 呼ばれています 忠実 、 もしも
呼ばれています 忠実 、 もしも  魅力はそうです Kofasernd 、 もしも
魅力はそうです Kofasernd 、 もしも  補助はです。
補助はです。  通常、次のモデルカテゴリ構造はトポロジールームと見なされます。
通常、次のモデルカテゴリ構造はトポロジールームと見なされます。 非陰性インデックスを持つR-Modulnの鎖複合体には、次のモデルカテゴリ構造があります。
非陰性インデックスを持つR-Modulnの鎖複合体には、次のモデルカテゴリ構造があります。
Recent Comments