セルビルドン – ウィキペディア

それ自体をたくさん描写するイラストは、数学の意味があります セルビルド層。 これらのイラストは、数学のすべての分野で重要な役割を果たします。一方で、この構造について自己反射の構造の構造を得ることができるという変化は、イラストを繰り返し使用して使用できないため、要素とその画像要素を直接比較できます。

構造的に真のまたは構造的な自己基準を通じて構造を記述する最初の概念は、フェリックス・クラインによってエルランゲンプログラムによって幾何学に最初に導入され、現代数学の最も肥沃なアイデアの1つです。アーキタイプとイメージの比較可能性、および自己形成の反復性に基づいている2番目の概念は、数字に不可欠であり、フラクタル幾何学の基本概念の1つです。

多分

${displaystyle a}$

任意の量。次に、関数が呼び出されます

${displaystyle alpha colon ato a}$

自己探求。 ^{[初め] [2]}

${displaystyle alpha}$

また、単一のdigitリンクを意味します

${displaystyle a}$

。

1. たくさんのアイデンティティ
   ${displaystyle a}$

   自己探求です。

   ${displaystyle id_ {a}コロンアトA; Amapsto a}$

   。

2. 自己探求を伴う量の最も重要な例はカウントされています。すべての自然数は後継者に割り当てられます。
   ${displayStyle 1+コロンMATHBB {n}からmathbb {n}; nmapsto 1+n}$

   。

3. 数字です
   ${displaystyle n}$

   10進システムに表示されるので、できます

   ${displaystyle q（n）}$

   に割り当てます。それもそうです

   ${displaystyle q（12345）= 15、q（15）= 6}$

   。一般的

   ${displaystyle textStyle qcolon mathbb {n} to mathbb {n}; sum _ {i = 0}^{k} a_ {i} cdot 10^{i} mapsto sum _ {i = 0}^{k} a_ {i}}}$

   。そうです

   ${displaystyle n}$

   正確に3で割り切れます

   ${displaystyle q（n）}$

   3で割り切れます。

4. そうです
   ${displaystyle mathbb {q} ^{+}}$

   正の合理的な数字の量と

   ${displaystyle alpha colon mathbb {q} ^{+} to mathbb {q} ^{+}; xmapsto {tfrac {1+x} {x}}}$

   自己探求。向きを変えたら

   ${displaystyle alpha}$

   たとえば、繰り返して出ます。

   ${displaystyle x = 1}$

   あなたからエピソードを手に入れます

   ${displaystyle 1mapsto 2mapsto {tfrac {3} {2}} mapsto {tfrac {5} {3} {3}} mapsto {tfrac {8} {5}} mapsto dotso}$

   。これらの骨折の結果として、カウンターと分母は連続したフィボナッチの選挙です。の

   ${displaystyle mathbb {r}}$

   このエピソードには限界値があります

   ${displaystyle phi = {tfrac {1+ {sqrt {5}}} {2}}}}$

   。これはゴールデンカットの数です。

内型と自動性 [ 編集 | ソーステキストを編集します ]

構造的補成性自己拡張は構造化されており、内膜と呼ばれます。このイラストも可逆的であり、反転イメージも構造的である場合、それは自動性と呼ばれます。これらの図に保存されている構造は、さまざまな数学的サブエリアで異なる場合があります。
代数では、通常、イラスト自体が構造的で可逆的であることを要求するだけで十分であり、逆転画像も構造的であるという事実をもたらします。

自動化と不変の構​​造の説明 [ 編集 | ソーステキストを編集します ]

たとえばベクタールームなど、非常に一般的な構造を想定しています の。 その結果、自動化グループの例では、リバーシブルイラストとしてグループを形成する基本的な量が、ベクター空間構造を尊重します。現在、距離や角度などの追加の構造が導入されています。これらの構造の1つ以上の要求 不変 自動化の下にある可能性があり、サブグループは元のグループで区別します。 Erlangenプログラムは現在、すべての「ジオメトリ」（疑わしい」（不変のシステムとして疑わしい）を、サブグループとその不変性を通じて自動化グループの完全なグループの副グループによる記述を提供しています。

理論物理学では、問題の対称性（グループ）からメンテナンスレート（不変）に至るまで、基本的なアイデアが使用されます。

要素または多くに同じ自己探求を適用し続けた概念は、一方でイラストの固定点の近似値を取得し、他方では、たとえばジオメトリで – グリッドやフラクタルなどの特定のクラスの量を定義します。

反復近似手順 [ 編集 | ソーステキストを編集します ]

実際の分析からの特別なケースは、収縮（数学）で説明されています。一般化はバナッハの固定点です。

定義「反復的な意味」 [ 編集 | ソーステキストを編集します ]

正式には、Erlangenプログラムのように、それは再び不変についてですが、ほとんどの場合、これらの定義は古典的な幾何学的関係の外で発生します。

定期的な数字

フィギュア

${displaystyle f}$

レベルでは、シフトによってそれ自体にマッピングされると定期的に呼び出されます。周期的な数値は、たとえば、三角関数の副鼻腔、Cosine、…グリッドの周期的な数値でもあります。対応する定義は、任意の次元のベクトルに困難なく転送できます。

フラクタルは考えています

フラクタル量は、自己類似の量です。つまり、類似性イメージによってそれ自体にマッピングされる、実際のベクトルまたは複雑なベクトルのサブ量です。ここで、自己探求（最終的に寸法の場合）は3つのフェーズです。

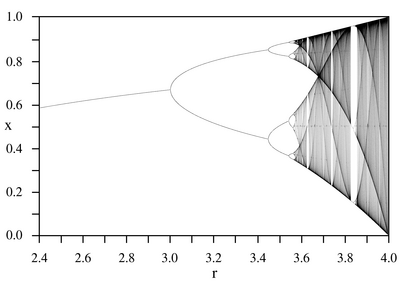
自己探知は、動的システムの研究において重要な役割を果たします。ロジスティックイラスト

${displaystyle varphi}$

多くのアプリケーションの例として役立ちます：

${displaystyle varphi（x）= rx（1- x）}$

と

${displaystyle 0leq xleq 1}$

と

${displaystyle 0leq rleq 4}$

グラフィックは、のクラスターポイントを示しています

${displaystyle x_ {n+1} = varphi（x_ {n}）}$

再帰的に定義されたエピソード

${displaystyle 0$

パラメーターの値に応じて反復シーケンスがわかります

${displaystyle r}$

収束することも、最終的に無限の数のクランプを持っています。最初の枝の前のエリアでは、自己茎の形成は

${displaystyle varphi}$

それどころか、あなたの限界は固定点とアトラクタです。全体としての図は、フラクタル構造を示しています。

1. ↑ Harro Heuser： 分析の教科書 。第17版。パート1. Vieweg+Teubner Verlag、2012、ISBN 978-3-8348-0777-9、 S. 106 。
2. ↑ エリック・W・ポインターシュタイン： セルフマップ 。 の： Mathworld （英語）。