立方機能 – ウィキペディア

Posted on April 1, 2020 by lordneo

before-content-x4

立方体関数のグラフ;ゼロポイント（y = 0）はグラフがあるところですバツ – イーンカット。グラフには2つの極端なポイントがあります。

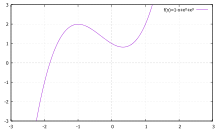
立方関数のグラフf（x）= 1-x+x²+x³

数学では1つを意味します 立方機能 3度目の完全な合理的関数、すなわち関数

{displaystyle fcolon mathbb {r} to mathbb {r}}

after-content-x4

$fcolon mathbb {R} to mathbb {R}$ 形にある実数について

{displaystyle f（x）= ax^{3}+bx^{2}+cx+d}

と

{displaystyle a、b、c、din mathbb {r}}

$a,b,c,din mathbb{R}$ と

{displaystyle aneq 0}

$aneq 0$ 書くことができます。

after-content-x4

立方機能は、ポリノムの実際の多項式機能として使用できます

{displaystyle mathbb {r}}

$mathbb {R}$ 理解されます。

Table of Contents

無限の行動 [ 編集 | ソーステキストを編集します ]

unchallow程度のすべての合理的な機能と同様

{displaystyle lim limits _ {xto +infty} f（x）= +infty}

主要な係数の場合

{displaystyle a}

$a$ ポジティブです

{displaystyle lim limits _ {xto +infty} f（x）= – infty}

滝

{displaystyle a}

$a$ ネガティブです。

ゼロポイント [ 編集 | ソーステキストを編集します ]

立方体関数は多項式関数として安定しているため、無限と中間値の挙動は、常に少なくとも1つの実際のゼロを持つことになります。一方、程度の合理的な機能全体ができます

{displaystyle n}

$n$ 以下

{displaystyle n}

$n$ 独自のゼロポイント。そのため、次のとおりです。立方体関数があります

{displaystyle mathbb {r}}

$mathbb {R}$ 少なくとも1つと最大3つのゼロポイント。

立方機能のゼロ点の発見については、Cardian方程式とカルダニアン式を参照してください。
一般的な立方機能の判別

{displaystyle f}

$f$ ケースです

{displaystyle d = b^{2} c^{2} -4ac^{3} -4b^{3} d-27a^{2} d^{2}+18abcd}

多項式のゼロポイント分類に適しています：場合

{displaystyle d> 0}

$D > 0″></span>ケースには3つの異なる実際のゼロポイントがあります <span class=$

{displaystyle d <0}

$D < 0$ 一つだけ。適用可能です

{displaystyled = 0}

$D = 0$ 、シンプルでダブルのリアルゼロポイントがあります。または、トリプルリアルゼロがあります。

関数グラフに実際のゼロポイントがある場合、次の方法で決定できます。

{displaystyle f（x）= ax^{3}+bx^{2}+cx+d}

{displaystyle nst = – {frac {b} {3a}} – {frac {1} {3a}} {sqrt [{3}] {b^{3} – {frac {9} {2}} {27} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} {2} l（} b^{3} – {frac {9} {2}} abc+{frac {27} {2}} a^{2} d {bigr）}^{2} – {bigl（} b^{2} -3ac）}^{3}}}}}}}}

{displaystyle-{frac {1} {3a}} {sqrt [{3}] {b^{3} – {frac {9} {2}} abc+{frac {27} {2}} a^{2} d- {{} {} {} {} {} {} {} {} {2}} abc+{frac {27} {2}} a^{2} d {bigr）}^{2} – {vigl（} b^{2} -3ac {bigr）}^{3}}}}}}}}}}}}}}}}}

平方根下の式は正です。

このゼロポイントフォーミュラは、正方形の真夜中のフォーミュラの立方類のアナログを形成します。

たとえば、ニュートンプロセスではゼロポイントの数値発見が可能です。

表現

{displaystyle {tfrac {b} {3a}}}

${displaystyle {tfrac {b}{3a}}}$ ページの算術平均を表します

{displaystyle a}

$a$ 、

{displaystyle b}

$b$ と

{displaystyle c}

$c$ それに匹敵する立方体

{displaystyle {tfrac {p} {2}}}

${displaystyle {tfrac {p}{2}}}$ ページの算術平均が

{displaystyle a}

$a$ と

{displaystyle b}

$b$ 長方形です。

立方体関数は、ゼロポイント形式として表すことができます。

{displaystyle f（x）=（x+a）（x+b）（x+c）}

ある

{displaystyle a}

$a$ 、

{displaystyle b}

$b$ と

{displaystyle c}

$c$ 立方体の側面。の前の要因

{displaystyle x^{3}}

$x^3$ 関数の勾配は、立方体の数または立方体の割合、前の因子に対応します

{displaystyle x^{2}}

$x^{2}$ 副量に対応し、前の因子

{displaystyle x}

$x$ 立方体の表面の半分と立方体のボリュームの定数に対応します。

{displaystyle f（x）= mx^{3}+（a+b+c）x^{2}+（ab+ac+bc）x+abc}

正方形関数の頂点形式に類似して、ターニングポイントは、立方体の追加の助けを借りてセットアップできます。

{displaystyle f（x）= left（x+{tfrac {a+b+c} {3}}右）^{3}+dx+e}

例

{displaystyle {begin {aligned} f（x）＆= x^{3}+9x^{2}+20x+12 \＆=（x+3）^{3} -7x-15 \ 7x+15＆=（x+3）^{3} end {aligned}}}}}}

最初のゼロは同じです

{displaystyle x = -3+2 = -1}

${displaystyle x=-3+2=-1}$ 、ターニングポイントはです

{displaystyle {tfrac {-3} {f（-3）}}}}

${displaystyle {tfrac {-3}{f(-3)}}}$ 、

{displaystyle b+c = 8 = p}

${displaystyle b+c=8=p}$ 、

{displaystyle bc = 12 = q}

${displaystyle bc=12=q}$ 。 2番目と3番目のゼロの位置は、正方形のサプリメントになります。

{displaystyle x = -3+1 = -2}

${displaystyle x=-3+1=-2}$ と

{displaystyle x = -3-3 = -6}

${displaystyle x=-3-3=-6}$ 。

単調と地元のエクストラ [ 編集 | ソーステキストを編集します ]

多項式機能として

{displaystyle f}

$f$ これ以上頻繁に異なります。あなたの最初の派生のために

{displaystyle f ‘}

$f'$ 正方形の関数の結果

{displaystyle f ‘（x）= 3ax^{2}+2bx+c}

彼らの判別です

{displaystyle 4b^{2} -12ac}

$4b^{2}-12ac$ ポジティブ、d。 H.適用されます

{displaystyle b^{2}> 3AC}

$b^{2}>3ac”></span>、だから所有しています <span class=$

{displaystyle f}

$f$ 正確にローカルの最大値と正確なローカル最小。そうでなければ

{displaystyle f}

$f$ 厳密に単調で、厳密に単調です

{displaystyle a> 0}

$a>0″></span>そして、厳密に単調です <span class=$

{displaystyle a <0}

$a<0$ 。

ターニングポイントと対称性 [ 編集 | ソーステキストを編集します ]

すべての立方機能

{displaystyle f}

$f$ ちょうど1つのターニングポイントがあります

{displaystyle（x_ {w}; f（x_ {w}）}

$(x_{W};f(x_{W}))$ 。ターニングポイント

{displaystyle x_ {w} = – {frac {b} {3a}}}}

2番目のデリバティブの明確に決定されたゼロポイントです

{displaystyle f ”（x）= 6ax+2b}

$f''(x)=6ax+2b$ 。

の機能

{displaystyle f}

$f$ 彼のターニングポイントと対称的なポイントです。

通常のフォーム [ 編集 | ソーステキストを編集します ]

シフトとスケーリングにより、すべての立方機能は

{displaystyle f}

$f$ ダイの形で

{displaystyle g（u）= u^{3}+house

と

{displaystyle kin {-1,0,1}}

$kin {-1,0,1}$ 持っていく。

したがって、この通常のフォームの3つの可能なケースを正確に取得します。：

${displaystyle k = -1}$
${displaystyle k = 0}$
${displaystyle k = 1}$

通常の形式での変換はextreemの存在を変えないため、この特性は元の関数にも適用されます

{displaystyle f}

$f$ 。
係数

{displaystyle k}

$k$ 元の関数の導出の判別の反対の兆候です

{displaystyle f}

$f$ 。

いつ 立方体のパラベル キュービック関数の関数グラフと、回転に起因するレベルの曲線を指す場合。曲線を見るときは翻訳は無関係であるため、立方体ポリノームのみが必要です

{displaystyle b = d = 0}

$b=d=0$ 分析的に調べる。

多分

{displaystyle r}

$R$ 任意のリング。立方体のポリノームが過ぎたように

{displaystyle r}

$R$ 1つはフォームの表現を指します

{displaystyle ax^{3}+bx^{2}+cx+din r [x]}

と

{displaystyle a、b、c、din r}

${displaystyle a,b,c,din R}$ と

{displaystyle anot = 0}

$anot =0$ 。正式には、それはグレード3の多項式リングの要素であり、彼らはの画像を定義します

{displaystyle r}

$R$ 後

{displaystyle r}

$R$ 。その場合

{displaystyle r = mathbb {r}}

${displaystyle R=mathbb {R} }$ 上記の感覚は立方機能です。

滝

{displaystyle r}

$R$ 代数的に閉じた身体は、すべての立方体多項式が3つの線形因子の積として崩壊します。

より一般的なのは、立方体ポリノームです

{displaystyle n}

$n$ フォームの可変式

{displaystyle sum _ {i、j、k = 1}^{n} a_ {i、j、k} x_ {i} x_ {j} x_ {k}+sum _ {i、j = 1}^{n} b_ {i、j} x_ {i} x_ {i} x_ {i}+sum+ } x_ {i}+din r [x_ {1}、ldots、x_ {n}]}

すべてではありませんが

{displaystyle a_ {i、j、k}}

${displaystyle a_{i,j,k}}$ ゼロである必要があります。
これらのポリノームはの画像を定義します

{displaystyle r^{n}}

$R^{n}$ 後

{displaystyle r}

$R$ 。彼らのゼロ位置

{displaystyle r^{n}}

$R^{n}$ のためになります

{displaystyle n = 2}

$n=2$ キュービック曲線として（曲線に楕円曲線として特異性がない場合）および

{displaystyle n = 3}

$n=3$ 立方地域と呼ばれます。

after-content-x4

after-content-x4