カタロニアザール – ウィキペディア

カタロニアの数 また カタロニアの数 組み合わせの多くの問題で発生する自然数の結果を形成し、二項係数またはフィボナッチ数と同様に重要な役割を果たします。彼らは、ベルギーの数学者のオイゲーヌ・チャールズ・カタロニア語にちなんで名付けられました。

カタロニアの数の結果

${displaystyle c_ {0}、c_ {1}、c_ {2}、c_ {3}、dotsc}$

から始まります

1、1、2、5、14、42、132、429、1430、4862、16796、58786、208012、742900、… A000108 OEISで）

カタロニアの数は向けられています

${displaystyle ngeq 0}$

によって与えられた

${displaystyle c_ {n} = {frac {1} {n+1}} {binom {2n} {n} {n}} = {frac {（2n）！} {（n+1）！、n！}}、}、}$

したがって

${displaystyle {tbinom {2n} {n}}}$

中央の二項係数はです。と

${displaystyle {tbinom {2n} {n+1}} = {tfraac {n} {n+1}} {tbinom {2n} {n}}}}}$

に相当する式を取得した場合

$MM Slavetle State — Happix 2 Refinee MJoy 2 repparent M H repparents MJoy 1 1-1親MJoy 1 1-1$

したがって、実際には整数のみを提供します。

中国のミンガトゥカタロニア人の人物は、三角関数（1730年代としての1730年代）の無限の列を最初に見つけましたが、1839年には本としてのみ出版されました）。

このエピソードの数字は、1751年にキリスト教のゴールドバッハへの手紙でレオンハルト・オイラーによってすでに説明されていました。 ^[初め] ヨハン・アンドレアス・フォン・セグナーは1758年に控訴式を見つけました。 ^[2] セグナーの記事の要約におけるオイラーの解決策。 ^[3] Johann Friedrich Pfaffが作成したより一般的なカウントタスクは、1795年のニコラウスファスを解決しました。 ^[4] 1838年と1839年のガブリエルラメ、 ^[5] オリンド・ロドリゲス、 ^[6] ジャック・ビネット ^{[7] [8]} eugèneCatalan ^{[9] [十]} 再び質問。 Eugen Nettoは1901年に公開された彼のリードを率いました 組み合わせの教科書 カタロニア語の数字。 ^[11]

オイラーは可能性の数、凸面を探していました

${displaystyle n}$

– 対角線を切り抜けて三角形（三角測量）にカットします。この番号はです

${displaystyle c_ {n-2}}$

。たとえば、五角形には5つの可能な三角測量があります。

1751年のゴールドバッハへの手紙（歴史を参照）で、オイラーは明示的な公式を与えました

${displaystyle c_ {n} = {frac {2cdot 6cdot 10dotsb（4n-2）} {2cdot 3cdot 4dotsb（n+1）}} = prod _ {k = 1}^{n} {frac {4k-2} {k+1}}}}}$

（*）

と式

${displaystyle sum _ {n = 0}^{infty} c_ {n} x^{n} = {frac {1- {sqrt {1-4x}}} {2x}} = {frac {2} {1+ {sqrt {1-4x}}}}}}}}}$

特に生成関数の場合

${displaystyle sum _ {n = 0}^{infty} {frac {c_ {n}} {4^{n}}} = 2}$

成長行動の説明としても。 ^[初め]

ガンマ関数で

${displaystyleガンマ}$

該当する：

${displaystyle c_ {n} = {frac {4^{n} gamma {left（{tfrac {1} {2}}+nright）}} {sqrt {pi}}、gamma {left（2+night）}}}}}}}}$

式から直接 （*） 続きます

${displaystyle c_ {n+1} = {frac {4n+2} {n+2}}、c_ {n}。}$

再帰式も適用されます（Segner 1758） ^[2]

${displaystyle c_ {n+1} = sum _ {k = 0}^{n} c_ {k}、c_ {n-k}、}$

たとえば、です

${displaystyle c_ {3} = c_ {0}、c_ {2}+c_ {1}、c_ {1}+c_ {2}、c_ {0}}$

。

別の再帰式があります

$M TUME SLEXLE STATE EMPASUXMéReporalKoror Horor M Hork2Kö2ok）マルメイト、Samlɔまたは22-25-$

Motzkin NumbersMと同様にM（シーケンス A001006 OEISで）

$MMS SLEPLE STATES STATEK？$

のすべての主要な要因から

${displaystyle textStyle c_ {n} = 2^{n}、{frac {1cdot 3cdot 5cdots（2n-1）} {2cdot 3cdot 4cdots（n+1）}}}}}}$

、式を参照してください （*）、 未満

${displaystyle 2n}$

and and

${displaystyle c_ {n}> 2n}$

${displaystyle n> 3}$

${displaystyle c_ {2} = 2}$

と

${displaystyle c_ {3} = 5}$

カタロニア語の唯一の数も一次数です。フォーミュラもそれを示しています

${displaystyle c_ {n}}$

その間の各プライム番号を通して

${displaystyle n+1}$

と

${displaystyle 2n}$

分裂しやすく、まったく奇妙です

${displaystyle n+1}$

2の効力です。

一致は、ウォルツステンホルムの文から続きます

${displaystyle（p、n+1）、c_ {p、n} equiv（n+1）、c_ {n} {pmod {p^{3}}}}}$

すべての素数用

${displaystyle p> 3}$

${displaystyle operatorname {mod} p^{4}}$

、プライム番号2と3に適用されます

${displaystyle operatorname {mod} p^{2}}$

。

特にそうです

${displaystyle c_ {p^{k} n} equiv（n+1）、c_ {n} {pmod {p}}}$

と

${displaystyle c_ {p^{k}} equiv 2 {pmod {p}}}$

すべての素数用

${displaystyle p}$

そして整数

${displaystyle k> 0}$

${displaystyle c_ {n} sim {frac {4^{n}} {（n+1）{sqrt {pi n}}}}。}。$

相互値の合計は収束します： ^[12番目]

${displaystyle sum _ {n = 0}^{infty} {frac {1} {c_ {n}}} = 2+ {frac {4 {sqrt {3}} pi} {27}}}}}}$

適用も適用されます（結果 A013709 OEIS 2016で）：

${displaystyle sum _ {n = 0}^{infty}左（{frac {c_ {n}} {2^{2n+1}}}右）^{2}（n+1）= {frac {1} {pi}}}}}}（n+1）= {$

としても

${displaystyle sum _ {n = 0}^{infty}左（{frac {c_ {n}} {2^{2n+1}}}右）^{2}（4n+3）= 1}$

${displaystyle sum _ {n = 0}^{infty}左（{frac {c_ {n}} {2^{2n}}}右）^{2}（n+1）= {frac {4} {pi}} = sum _ {n = -1}^{{{_ {{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{）{{{{{{{{{{{{{{{{{{ce）） 2^{2n+1}}}右）^{2}}$

（Wallis Lambertシリーズ）

${displaystyle c _ { – 1} = – {frac {1} {2}}}$

バーゼルの問題を伴うCauchy製品の式は、これに起因します（結果 A281070 OEIS 2017で）：

${displaystyle sum _ {n = 0}^{infty} sum _ {k = 0}^{n}左（{frac {k_ {k}} {2^{2k+1}}}右）^{2} {frac {k+1} {{n-k+1）}} {{k+1} 6}}}$

カタロニアの数は、グラフ理論的にカウントされた木である多数のカウントタスクで発生します。そうです

${displaystyle c_ {n}}$

の数

たとえば、あなたはする必要があります

${displaystyle n = 3}$

のような文字列

${displaystyle x*x*x*x}$

5つの異なる方法で可能なブラケットに設定してください。

${displaystyle（（x*x）*x）*xqquad（x*（x*x））*xqquad（x*x）*（x*x）qquad x*（（x*x）*x）qquad x*（x*x）}$

減算の明示的な例は次のとおりです

${displayStyle（（10-6）-3）-1QQuad（10-（6-3））-1QQuad（10-6） – （3-1）QQUAD 10-（（6-3）-1）QQUAD 10-（6-（3-1））}$

それが理由です

${displaystyle c_ {3} = 5}$

。括弧内または完全な表現の周りに既に設定された式に冗長ブラケットを追加することは許可されていません。 0ノットのバイナリツリーがあり、他のすべてのバイナリツリーは、その左右の部分ツリーの組み合わせによって特徴付けられます。これらのサブツリーの場合

${displaystyle i}$

また。

${displaystyle j}$

結び目があり、木全体にあります

${displaystyle i+j+1}$

ノード。したがって、番号

${displaystyle c_ {n}}$

バイナリツリーから

${displaystyle n}$

次の再帰的な説明を結びます

${displaystyle c_ {0} = 1}$

と

${displaystyle textStyle c_ {n} = sum _ {i = 0}^{n-1} c_ {i} cdot c_ {n-1-i}}$

すべての正の数に対して

${displaystyle n}$

。それに続きます

${displaystyle c_ {n}}$

インデックス付きのカタロニア番号

${displaystyle n}$

は。これは、たとえば、非共同マトリックスチェーン乗算における計算シーケンスの数の数の尺度であり、巧みに最適化された留め金によって計算の取り組みを最小限に抑えることができます。

• その後0からの次元のワンダラー
  ${displaystyle 2n}$

  開始とエンドポイントが0で、パスが決して

  ${displaystyle x}$

  -achsはあります（DyckからWaltherへのいわゆるDyckパス）。たとえば、です

  ${displaystyle c_ {3} = 5}$

  、あらゆる種類のパスは次のとおりです。

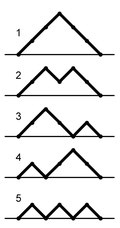
• 正方形のグリルの端に沿った単調な経路
  ${displaystyle n}$

  対角線の上の点を含んでいない二次細胞。単調なパスは左下隅から始まり、右上隅で端が終わり、右または上に表示される端から完全に構成されています。 14の単調なパス

  ${displaystyle n = 4}$

  それは： ^[13]

• 幅の段階的な形をとる機会
  ${displaystyle n}$

  と高さ

  ${displaystyle n}$

  と

  ${displaystyle n}$

  長方形を傾けるタイル。の14のオプション

  ${displaystyle n = 4}$

  それは： ^[13]

• 候補者Aが候補者Bの背後に決してないことをカウントする選挙でカウントする可能性のあるコース
  ${displaystyle n}$

  受け取った声と投票用紙は、骨nから連続して数えられます。たとえば

  ${displaystyle n = 2}$

  前提条件を満たす描画の可能性のある結果です。 ^[14]

• 方法の可能性
  ${displaystyle 2n}$

  丸いテーブルに座っている人は、腕を交差せずにテーブルの上に手を置きます。 ^[14]

• ピーターJ.ヒルトン、ジャンペダーセン： 整数グリッド内のカタロニアの数とパス。 数学の要素48、1993、 doi：10.5169/seals-44624＃51 、S。45ff。
• JürgenSchmidthammer： カタロニアの数。 （PDFファイル; 7.05 MB）、州試験の入場作業、1996年2月Erlangen。
• トーマス・コシ： アプリケーションを備えたカタロニアの数。 オックスフォード大学出版局、ニューヨーク2009、ISBN 978-0-19-533454-8。
• リチャード・P・スタンリー： 列挙組み合わせ。 第2巻、ケンブリッジ大学出版局、ケンブリッジ1999、ISBN 0-521-56069-1（英語;カタロニア語の解釈に関する継続的に更新されたリストを備えた本のスタンリーのウェブサイト： 列挙組み合わせに関する情報 ）。

1. ↑ ^{a b} 簡単に （PDFファイル; 137 kb）1751年9月4日のオイラーからゴールドバッハまで、ポールハインリッヒファス（編）で印刷： いくつかの有名な18世紀の測量士の数学的および身体的通信。 （バンド1）、聖ペテター1843、 S. 549–552。
2. ↑ ^{a b} IOH。アンドル。彼らは播種： 対角線における直腸肉肉体の数字が三角形に分割される方法の列挙 。 1758年と1759年、1761年、S。203-210（Deutsch）の新しい解説アカデミー7。
3. ↑ Leonhard Euler： 概要論文 。 1758年と1759年、1761年、新しい解説アカデミー7科学アカデミー7 13–15 （ラテン語）。
4. ↑ ニコラス・ファス： 質問の解決策、ポリゴナm側のポリゴナムnレンガの方法の数、対角線によって解決された 。 Acta Nova 9、1795、S。243-251（Deutsch）。
5. ↑ ガブリエル・ラメ： この質問について、ラメ氏からリウヴィル氏への手紙から抜粋します。 純粋および応用数学ジャーナル3、1838、S。505–507（Französisch）。
6. ↑ オリンド・ロドリゲス： 対角線を使用してポリゴンを三角形に分解する方法の数について と 要因を実行する方法の数について 。 純粋および応用数学ジャーナル3、1838、S。547–549（Französisch）。
7. ↑ J.ビネット： ポリゴンの問題 。 Sociétéのフィロマティックデパリセッションの1838年の抽出物、S。127–129（Französis）。
8. ↑ J.ビネット： 直線的な数字をその対角線によって三角形で共有できる方法の数を決定する問題についての反映 。 純粋および応用数学新聞4、1839、S。79–90（Französisch）。
9. ↑ ^{a b} E.カタラン： 完成した違いのある方程式に注意してください。 純粋で応用された数学ジャーナル3、1838、S。 508–516 、および4、1838、p。 95–99 （フランス語）。
10. ↑ E.カタラン： この質問の新しい解決策：与えられたポリゴン、対角線を使用して三角形で共有する方法はいくつありますか？ Journal of Pure and Applied Mathematics 4、1839、S。91–94（Französisch）。
11. ↑ Eugen Net： 組み合わせの教科書 。 B. G. Teubner、Leipzig 1901（§122、pp。192–194および§124、p。195のカタロニアへの数字の復帰）。
12. ↑ 相互のカタロニア数の全額。 で： juanmarqz.wordpress.com。 2009年7月29日、2021年1月11日アクセス。
13. ↑ ^{a b} Matej Crepinsek、Luka Mernik： カタロニアの数関連の問題を解決するための効率的な表現。 （PDF; 253 kb）。の： ijpam.eu。 2021年1月11日にアクセスされた純粋および応用数学の国際ジャーナル。
14. ↑ ^{a b} doina logofatu： C ++を使用したアルゴリズムと問題ソリューション。 第8章 カタロニアの数。 Vieweg-Verlag、第1版2006、ISBN 978-3-8348-0126-5、pp。189–206。