マイナー（graphentheorie） – ウィキペディア

グラフ理論で マイナー エッジの収縮とエッジまたはノットを省略することにより、異なるグラフから取得できる特定のグラフ。サブグラフの関係と区画関係に加えて、マイナーな関係はグラフ理論の間の最も重要な関係の1つであり、次のような詳細な文で多くのことを可能にします。 B. KuratowskiまたはRobertson and Seymourのマイナー定理の刑。

言及されたすべてのグラフは常に簡単です。

マイナー [ 編集 | ソーステキストを編集します ]

ノードを交換する場合

${displaystyleをお願いしますv}$

グラフ

${displaystyle g}$

分離接続されたグラフを介して

${displaystyle g_ {x}}$

エッジと同様に

${displaystyle xy}$

終えた

${displaystyle g_ {x}}$

–

${displaystyle g_ {y}}$

– エッジ、それはあなたが新しいグラフを取得する方法です

${displaystyle ig}$

呼ばれています（

${displaystyle i}$

膨らむため）。この名前は、元のグラフがノードの置換により大きいという事実につながります。これでグラフが含まれています

${displaystyle with}$

a

${displaystyle ig}$

、男と言う

${displaystyle g}$

a マイナー から

${displaystyle with}$

。

Topogischerマイナー [ 編集 | ソーステキストを編集します ]

は

${displaystyle g}$

グラフ、それがグラフの名前です

${displaystyletg}$

区画グラフ から

${displaystyle g}$

、エッジによって細分化されている場合

${displaystyle g}$

出現しました。のノード

${displaystyletg}$

、誰も

${displaystyle g}$

その後、含まれます 分岐ノード 呼び出されると、他のすべてのノットが呼ばれます 区画ノード。 分岐ノードは学位を継承します

${displaystyle g}$

、サブディビジョンノードはすべてグレード2です。グラフが含まれています

${displaystyle with}$

区画グラフ

${displaystyletg}$

グラフ

${displaystyle g}$

、男と言う

${displaystyle g}$

a トポロジーマイナー から

${displaystyle with}$

。

同等の定義 [ 編集 | ソーステキストを編集します ]

次の定義は、文献に時々見つけることができます。

マイナー

グラフ

${displaystyle g}$

呼ばれています マイナー から

${displaystyle with}$

、 もしも

${displaystyle with}$

エッジ収縮によりサブグラフが含まれています

${displaystyle g}$

現れます。

Topogischerマイナー

グラフ

${displaystyle g}$

呼ばれています Topogischerマイナー から

${displaystyle with}$

、 もしも

${displaystyle with}$

の区画グラフ

${displaystyle g}$

含む。

マイナー [ 編集 | ソーステキストを編集します ]

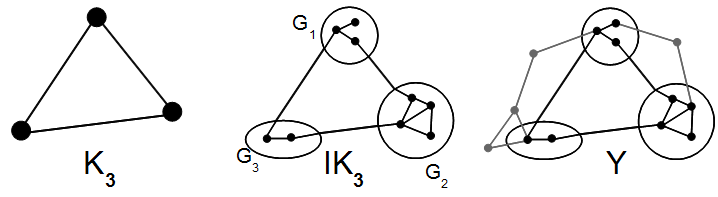
左側には3つのノットの完全なグラフがあります

${displaystyle k_ {3}}$

表示されています。これは、グラフからのエッジ収縮によって作成されます

${displaystyle ik_ {3}}$

誰が順番に

${displaystyle y}$

含まれています。

${displaystyle k_ {3}}$

マイナーもそうです

${displaystyle y}$

。

Topogischerマイナー [ 編集 | ソーステキストを編集します ]

3つのノードを備えた完全なグラフは、左側の区画グラフの中央に表示されます。サブディビジョングラフはグラフにあります

${displaystyle with}$

含む、

${displaystyle k_ {3}}$

トポロジーマイナーもそうです

${displaystyle with}$

。

Topogische Minoren [ 編集 | ソーステキストを編集します ]

グラフ

${displaystyle h}$

意志として Topogischerマイナー グラフ

${displaystyle g}$

のサブディビジョングラフの場合と呼ばれます

${displaystyle h}$

のサブグラフの等量

${displaystyle g}$

は。すべてのトポロジマイナーも未成年者であることがわかります。ただし、逆転は一般的には適用されませんが、最大3のノードを持つグラフに適用されます。完全なグラフ。

${displaystyle k_ {5}}$

Petersen-Graphは未成年者ですが、トポロジーマイナーではありません。トポロジーマイナーな関係は、有限グラフの量についてはよく順序ではありません。したがって、ロバートソンとシーモアのマイナーな定理は、トポロジーマイナーには適用されません。 ^[初め]

未成年者 [ 編集 | ソーステキストを編集します ]

グラフ

${displaystyle h}$

意志として 誘導マイナー グラフ

${displaystyle g}$

誘導されたサブグラフからそれを記述します

${displaystyle g}$

一緒に引っ張ることで得ることができます。そうでなければ彼はそうするでしょう

${displaystyle h}$

– 介入され、未成年者から無料と呼ばれます。

イマージョンの未成年者 [ 編集 | ソーステキストを編集します ]

そのグラフ手術 リフト 概念の中心と呼ばれます 没入 と呼ばれます。リフティングは隣接するエッジで行われます。 3つのノット付き

${displaystyle v、u}$

と

${displaystyle in}$

、それによって

${displaystyle（v、u）}$

と

${displaystyle（u、w）}$

グラフのエッジ、の持ち上げです

${displaystylevuw}$

またはに相当します

${displaystyle（v、u）、（u、w）}$

2つのエッジの操作

${displaystyle（v、u）}$

と

${displaystyle（u、w）}$

削除され、エッジ

${displaystyle（v、w）}$

追加した。その場合

${displaystyle（v、w）}$

すでに存在していました、ノード

${displaystyle v}$

と

${displaystyle in}$

現在、複数のエッジで接続されているため、この手術自体はマルチグラフ手術です。

グラフがある場合

${displaystyle h}$

グラフから

${displaystyle g}$

持ち上げ操作の結果によって取得でき、その後、同型サブグラフが見つかります

${displaystyle h}$

a 没入マイナー から

${displaystyle g}$

は。浸漬操作に相当する没入マイノールを定義する別の方法があります。私たちはそれを言います

${displaystyle h}$

没入マイナー

${displaystyle g}$

ノードの無視の図がある場合です

${displaystyle h}$

結びつきます

${displaystyle g}$

隣接する要素の写真が贈られます

${displaystyle h}$

の

${displaystyle g}$

エッジによって接続されていますが、ジャンクです。

没入マイナーな関係は、有限グラフの量の適切な秩序であり、したがって、ロバートソンとシーモアのマイナーな定理は没入未成年者に適用されます。

グラフィック図面に関しては、非平面グラフの平面化として浸漬マイノが発生します。各交差点を新しい結び目に置き換えることにより、交差点でレベルのグラフの図面から没入マイナーを形成でき、すべての交差エッジがパスに分割されます。これにより、平面グラフの描画方法を非平面グラフに拡張できます。 ^[2]

奇数 [ 編集 | ソーステキストを編集します ]

未成年者の代替と同等の定義はそれです

${displaystyle h}$

マイナー

${displaystyle g}$

のノードの場合です

${displaystyle h}$

ノットを収集することにより – の部分的な木をケースします

${displaystyle g}$

2つのノットが入ったときに表現できます

${displaystyle h}$

隣接して、対応する2つのツリーにエンドノードがあるエッジ

${displaystyle g}$

存在した。

不変のマイナーは、これらのサブツリーにパリティ条件を追加することにより、この定義を制限します。もしも

${displaystyle h}$

上記のように、のサブツリーのコレクション

${displaystyle g}$

表示されます

${displaystyle h}$

より少ないマイナー

${displaystyle g}$

可能であれば、の結び目

${displaystyle g}$

の各エッジがの2つの色を割り当てます

${displaystyle g}$

エンドノードの色は異なり、各エッジが異なるため、部分ツリー内で正しく色付けされています。

${displaystyle g}$

、2つのサブツリーの間の近隣を表し、単色です。つまり、両方のエンドノードの色は同じです。通常のタイプの未成年者とは異なり、禁じられた奇妙な未成年者のグラフは必ずしも薄くはありません。 ^[3] ハドワイガーの仮定

${displaystyle k}$

– クロマティックグラフは必然的にグラフを完了します

${displaystyle n}$

未成年者としてのノードが含まれていることも、Unastersの観点からも調べられました。 ^[4]

マイナーな二部 [ 編集 | ソーステキストを編集します ]

未成年者の定義のもう1つの拡張は、元のグラフが二部であるときに二部グラフを生成する二部未成年者の概念です。グラフ

${displaystyle h}$

別のグラフのバイパルティイトマイナーです

${displaystyle g}$

、 もしも

${displaystyle h}$

out

${displaystyle g}$

ノットを取り外し、エッジを取り外し、グラフの周辺サイクルに沿って互いに距離2を持つエッジ収縮を採取することで保存できます。ワーグナーの文の形式は二部の未成年者に適用されます：二部グラフはそれがあれば平面グラフです

${displaystyle k_ {3,3}}$

二部はありません。 ^[5]

1. ↑ グーリディン： マイナーの長い二重経路を除く 。の： Journal of Combinatorial Theory 。 バンド 66 、 いいえ。 初め 、1996、 S. 11–23 、doi： 10.1006/jctb.1996.0002 。
2. ↑ クリストフ・ブッフハイム、マルクス・チマーニ、カルステン・ガトウェンガー、マイケル・ユンガー、ペトラ・ムッツェル： グラフの描画と視覚化のハンドブック 。 CRC Press、Boca Raton、FL 2014。
3. ↑ Ken-ichi Kawarabayashi, Yusuke Kobayashi, Bruce Reed: 二次時代のばらばらのパスの問題 。の： Journal of Combinatorial Theory 。 バンド 102 、 いいえ。 2 、2012年3月、 S. 424–435 、doi： 10.1016/j.jctb.2011.07.004 。
4. ↑ ジム・ジーレン、バート・ジェラード、ブルース・リード、ポール・シーモア、エイドリアン・ベッタ： Hadwigerの推測の奇妙な変種について 。の： Journal of Combinatorial Theory 。 バンド 99 、 いいえ。 初め 、2009年、 S. 20–29 、doi： 10.1016/j.jctb.2008.03.006 。
5. ↑ ギル・カライのマリア・チュドノフスキーは、ネボ、イザベラ・ノビク、ポール・シーモアでした： 二部未成年者 。の： Journal of Combinatorial Theory 。 バンド 116 、2016、 S. 219–228 、doi： 10.1016/j.jctb.2015.08.001 、arxiv： 1312.0210 。