Balkentherior-ウィキペディア

Posted on February 1, 2022 by lordneo

before-content-x4

バルケン理論 ストレス下のバーの動作について説明します。これは、技術的なメカニズムのサブエリアです。特に、バーの弾性ベンドは、強度理論と弾力性の教えの助けを借りて調べられます。そのため、 Biegetheorie des Balkens 話す。

after-content-x4

土木工学および機械工学の工学に開発および適用されます。

曲げモーメントに加えて、応力サイズも縦方向および横方向の力、およびねじれの瞬間です。ベンドは、バーのジオメトリ（断面、おそらく長さを超えて）とその保管、およびバー材料の弾力性にも依存します。材料の強度値は、プラスチック製の曲がりと曲げ胸への移行を決定します。

バルケン理論は、時間とともに徐々に洗練されてきました。曲げプロセスはますます良くモデル化されましたが、理論の取り扱いはより複雑でした。ほとんどのアプリケーションでは、 古典的なビーゲル ^[初め]（理論I.順序）十分に正確な結果を計算しました。

Table of Contents

近似ステップ [ 編集 | ソーステキストを編集します ]

一般に、区別が行われます

一次バルケン理論: ビーム要素は均一なバーで考慮され、力と瞬間はバランスが取れています。ほとんどの場合、結果は現実と一致します。（I. A.、ニックの負荷が理想的なキンク圧力の10％未満の場合。）
二次バルケン理論を線形化: 変形したバーでは、ビーム要素が考慮されます。数学モデルは線形化されています。安定性の問題、および0.1バイクの回転角度への傾斜の大きな偏向に必要です。 ^[2]
3次のバルケンシー理論: 変形したバーでは、ビーム要素が考慮されます。数学モデルは線形化されていません。特別な場合には、約20°以上の非常に大きな偏向と傾向が必要です。

文献に応じて、非線形の用語を2次バルケン理論でも考慮することができます。そのため、第二政党の理論と第三者の理論の境界は流動的です。

古典的な仮定：Bernoullischeの仮定 [ 編集 | ソーステキストを編集します ]

Bernoullischesの内容は次のとおりです。

after-content-x4

バーはです スリム ：その長さは、その横断的寸法よりもはるかに大きいです。
変形前のバー車軸に垂直であったビーム交差セクションも、変形後の変形したバー軸に垂直です。
交差は、変形後も残ります。
曲げ変形は、バーの長さと比較して小さい（クロスセクション寸法のサイズの最大サイズ）。
バーは等方性材料で作られており、Hoke Lawに従います。

1人が話します Euler-Bernoulli-Balt 。ただし、これらは実際のバーでは多かれ少なかれ正確なモデルの仮定です。現実の世界には、このモデルに正確に対応するバーはありません。

2番目と3の仮定iが発生しますi。 A.重荷の梁の場合は決してありませんが、仮定/エピソード2.および3.が近似で許可されている場合、z。 B.キーワードTimoschenko-Balkenの下で処理されるバー。

ひずみが縦方向に除外されている場合、I。stabt理論のスタッフは、強度の基準（通常の力と曲がりに従って）に従って失敗する可能性があります。 Stabt Theory IIの順序では、この強度の基準は変形した状況で満たされなければなりません。これにより、横方向の曲がり（キンク）による安定性障害に関する声明が可能になります。
さらに、クロスフォースによる故障は、ベルヌーイ梁からも除外されています。

ちなみに、ビームは、多くの場合、全長（一定の交差セクション、弾性モジュールなど）にわたって一定の交差分野を持ち、数学的に使いやすいためです。

一次理論：statics [ 編集 | ソーステキストを編集します ]

古典的な理論は、本質的に一次理論と一致し、それにより、理論で必要とされる均一なビームの交差領域の平衡条件で動作します。

静的決定 [ 編集 | ソーステキストを編集します ]

静的に決定されたビーム

静的に決定された梁の場合、バランス条件からの支持力と切断サイズを決定できます。
静的に覆われた ^[3]^[4]^[5]平衡状態に加えて、サポート力とカットを決定できるようにするには、ビームも満たさなければなりません。
最も単純な場合、バーは、線形の不均一な微分方程式である豆線の方程式に基づいて計算されます。たわみの間の接続を確立します

{displaystyle in}

$w$ （の

{displaystyle with}

$z$ 方向）およびクロスロード（ルート負荷

{displaystyle q}

$q$ 、キャリア全体の個々の負荷、単一の瞬間、…）座標の関数として

{displaystyle x}

$x$ バー軸に沿って。

{displaystyle（ei（x）、w ”（x）） ” = q（x）}

剛性 [ 編集 | ソーステキストを編集します ]

剛性曲率に関連して曲げモーメントの大きさを示します。均一な交差セクションの場合、製品になります

{displayystle not}

$EI$ 弾性モジュールから

{displaystyle e}

$E$ 材料と幾何学的領域の慣性モーメントのモーメント

{displaystyle i}

$I$ 与えられた交差セクションの。後者はとして計算されます

{displaystyle i_ {y} = int z^{2} {rm {d}} a = iint z^{2} {rm {d}} y、{rm {d}} zquad}

長方形の交差セクションを備えたバーの場合

{displaystyle bcdot h}

$b cdot h$ （の

{displaystyle y}

$y$ – それぞれ

{displaystyle with}

$z$ -direction）is

{displaystyle i_ {y}（x）= int _ { – h（x）/2}^{h（x）/2} int _ { – b（x）/2}^{b（x）/2} z^{2} {rm {d}} y、{rm {d} {x} {x} x^{3 {x 12}}

ランドおよび移行条件は、サポートの種類に起因し、運動学的境界条件と動的（強度に関連する力と瞬間）で構成されます。

動的境界条件の場合、それはたわみとカットの間の接続に関連しています。

二gegemoment：

{displaystyle m（x）= -ei（x）、w ”（x）}

Querkraft：

{displaystyle q（x）= – （ei（x）、w ”（x） ‘}

曲げ電圧 [ 編集 | ソーステキストを編集します ]

曲げモーメントは曲げ緊張で構成され、これらは軸方向の方向にあります – ロッド上で変化する通常の電圧の分布を持つ緊張があります。

最も単純な場合、交差セクションを必要とするBernoullitheoryは、線形弾性材料の挙動と組み合わせて想定されます。この単純化は、式につながります。

{displaystyle sigma _ {b}（x、y、z）= – {frac {m_ {z}（x）cdot i_ {y}（x）+m_ {y}（x）cdot i_ {yz}（x）} {i_ {y}（x }} cdot y+{frac {m_ {y}（x）cdot i_ {z}（x）+m_ {z}（x）cdot i_ {yz}（x）} {i_ {y}（x）cdot i_ {z}（x） – （x）}}}}}}}}}}}}

偏差モーメントの場合i _YZ電圧共有によると、ゼロの後に曲がりが続きます。

{displaystyle sigma _ {b}（x、y、z）= {frac {m_ {y}（x）} {y_ {y}（x）}}}}（z}（x）}（x）} {i_ {z}}}}}}}}}}}

その中にあります

{displaystyle i}

$I$ 曲げ瞬間が回転する軸の周りの交差点の責任の瞬間。特徴的な値

{displaystyle i/z}

$I/z$ 最大で

{displaystyle with}

$z$ （交差セクションの最も外側の繊維）は抵抗モーメントとも呼ばれます

{displaystyle in}

$W$ 。非常によく知られている結果が続きます：バーの負荷容量はに比例します

{displaystyle i/hpropto bcdot h^{2}}

${displaystyle I/hpropto bcdot h^{2}}$ 。

さまざまなサポート位置の均等にストレスの多いバーの曲げ（非常に過剰）。青：ベッセルポイントの保管

非対称交差セクションの場合、座標系は、ベンドを両方向に個別に計算できるように、主な慣性軸の方向に回転する必要があります。例：Lプロファイルが上からロードされている場合、通常は直接直接側面に向きます。主要な契約軸のいずれかの方向にのみ、負荷の方向でのみバーを曲げます。

バーの曲がりがどれほど強く、サポートの位置に大きく依存しています。均一な負荷で

{displaystyle q（x）}

$q(x)$ = constは、微分方程式から最適な倉庫位置として取得されます。

曲げ電圧 特に、交差セクション（例えばバー）に作用する力は、膨張方向に垂直にロードされていることを説明しています。

ビームクロスセクションの通常の電圧は次のとおりです。

{displaystyle sigma（x、y、z）= {frac {n（x）} {a（x）}} – {frac {z}（x）cdot i_ {y}（x）+m_ {y}（x）cdot i_ {yz}（x）} {y_ {x） – x（x） – x（x） – {x）} {yz}（x））^{2}}} cdot y+{frac {m_ {y}（x）cdot i_ {z}（x）+m_ {z}（x）cdot i_ {yz}（x）}（x）} {i_ {y}（x } cdot z}

偏差のモーメントがゼロであり、通常の力なしでZ方向に単純な曲がりがある場合：

{displaystyle sigma（x、z）、= {frac {m_ {y}（x）} {i_ {y}（x）}} cdot z}

瞬間mです _と陽性、mで曲げるときに発生します _とために

{displaystyle with}

$z$ > 0列車と

{displaystyle with}

$z$ <0圧力電圧。 Mによる純粋な曲げ使用の場合に発生する量の最大の電圧は _としたがって、最も外側の繊維で

{displaystyle | z | _ {mathrm {max}}}

${displaystyle |z|_{mathrm {max} }}$ の上。

抵抗の瞬間

{displaystyle in}

$W$ 純粋な交差点値であり、攻撃モーメントの比率を関連する緊張と

{displaystyle sigma、}

$sigma,$ 「クリティカル」ファイバー

{displaystyle w_ {u}（x）= {frac {y_ {y}（x）} {z_ {mathrm {max}}（x）}}} ,, quad w_ {o}（x）= {frac {i_ {y}}}} {mitrm}}}}}}}}}}}}}}

説明します

{displaystyle i}

$I$ 慣性の瞬間。最大曲げ電圧の場合、次のようになります。

{displaystyle | sigma | _ {mathrm {max}}（x）= {frac {| m（x）|} {| w（x）| _ {mathrm {min}}}}}}}

抵抗モーメントの量が大きいほど、エッジファイバーの曲げ電圧の量が小さくなります。

獣の切り欠き、曲げ瞬間の汚染の下で曲がっているm

バーを曲げると、列車側に横たわっている縦方向の繊維（前面の写真の前面、左の部分画像）と圧力側に横たわっている（写真の背面、左側）。列車の応力は、伸びた繊維の浸漬圧力電圧で作成されます。最大プルから内側の最大圧力応力への電圧プロセスはiです。 d。 R.非線形ですが、線形分布は頻繁な仮定です。

比較的小さな曲がり角と正常な力がないため、ニュートラル（電圧 – フリー）繊維は、ビームの高さの中央にあります。断面領域の引張電圧と圧力は、通常の力がない限り、量の点で同じです。

Biegelinie des Balkenens [ 編集 | ソーステキストを編集します ]

偏向（たわみ）

{displaystyle in}

$w$ その代わりにバーの

{displaystyle x}

$x$ 次の線形微分方程式で説明できます。

{displaystyle w ”（x）= – {m_ {y}（x）over ei_ {y}}。}

曲げ瞬間の負担に依存します

{displaystyle m_ {y}（x）}

$M_{y}(x)$ 、慣性の瞬間

{displaystyle i_ {y}}

$I_{y}$ ビーム交差セクションと弾性モジュールの

{displaystyle e}

$E$ ビーム材料の（インデックス

{displaystyle _ {y}}

${displaystyle _{y}}$ ：クロス車軸の周りを曲げます

{displaystyle y}

$y$ ）。
最初の統合により、傾向が続きます

{displaystyle in ‘}

$w'$ 曲率からの豆線

{displaystyle in ”}

$w''$ ：

{displaystyle w ‘（x）= – {{int _ {0}^{x} m_ {y}（xi）、mathrm {d} xi +c_ {1}}

2番目の統合では、ビーゲルラインの傾向が豆ラインの傾向から生じます

{displaystyle in}

$w$ ：

{displaystyle w（x）= – {{int _ {0}^{x}（int _ {0}^{x} m_ {y}（xi）、mathrm {d} xi +c_ {1}）、mathrm {d} xi +c_ {2}}}}}

2つのサポート、中央強度汚染のビーム

{displaystyle p}

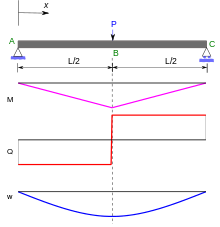
2つのエンドビーム（下の写真）を備えたビームの例では、曲げモーメントのコースにはねじれがあります。この場合、統合は通常、左と右のボークセクション用です ^[8]個別に実行されます。着実にビーゲリンラインの2つの結果の合併は、その傾向とたわみの両方が両方の部分で同じであるという事実から生じます。この例では、対称性（Bean Line and Moments Line）が利用可能です。統合z。 B.微分方程式は左半分に十分です。この半分は、強度で中央と反対側でも固定することができます

{displaystyle p/2}

${displaystyle P/2}$ （サポートにより）積み込まれたカンチレバービームを表示します。

ために

{displaystyle xleq l/2}

${displaystyle xleq L/2}$ 有効です：

{displaystyle m（x）= px/2、}

{displaystyle w ‘（x）= – {px^{2}/4+c_ {1} over ei_ {y}}、}

{displaystyle w（x）= – {px^{3}/12-pcdot l^{2} x/16+c_ {2} over ei_ {y}}、}

{displaystyle w（x）= {p（l^{2} x/16-x^{3}/12）over ei_ {y}}}}}

一次理論：ダイナミクス [ 編集 | ソーステキストを編集します ]

ここまでは、統計のみが扱われています。ビーム振動を計算するなどのバーのダイナミクスは、方程式に基づいています

{displaystyle（ei（x）、w ”（x、t）） ”+b、{dot {w}}（x、t）+m、{ddot {w}}（x、t）= q（x、t）}

問題はここの場所だけに依存するのではありません

{displaystyle x}

$x$ 、ただし、時間から

{displaystylet}

$t$ あちらへ。バーにはさらに2つのパラメーターがあります。つまり、質量分布

{displaystyle m}

$m$ そして構造減衰

{displaystyle b}

$b$ 。コンポーネントが水の下で振る場合は、含まれています

{displaystyle m}

$m$ また、流体力学的質量、および

{displaystyle b}

$b$ 線形化された形式の流体力学的減衰に含めることができます。モリソン方程式を参照してください。

二次の理論：キンクロッド [ 編集 | ソーステキストを編集します ]

これまでのところ、力と瞬間は均一な成分に伴っていましたが、キンクの場合、変形状態のバー要素を考慮する必要があります。 Knickstabの計算は、方程式に基づいています

{displaystyle（ei（x）、w ”（x）） ”+（n、w ‘（x））’ = q（x）}}

で最も単純な場合

{displaystyle q = 0}

$q=0$ 。これに追加されたのは、軸方向に作用する圧力力です

{displaystyle n}

$N$ 、境界条件に応じて、ロッドが曲がらないようにニックの荷重を超えてはなりません。

差別的な関係

バルケン理論のプッシュソフト理論ⅱ。順序は、ベルヌーリッシュの仮定の間のクロス共有の次の微分方程式です。

${displaystyle {frac {mathrm {d} r（x）} {mathrm {d} x}} = -q（x）}$

${displaystyle {frac {mathrm {d} m（x）} {mathrm {d} x} = r（x）-n^{ii}（x）cdot left [{d} w_ {v}} {d} x} {d} x} {d} {d} {d} {d} {d} {d} {d} {d} {d} {d} {d} {d} {d} {d} x}}右]+m（x）}$

${displaystyle {frac {mathrm {d} varphi（x）} {mathrm {d} x}} = – left [{frac {m（x）} {ecdot i（x）}}+kappa ^{e}（x）}}}}$

${displaystyle {frac {mathrm {d} w（x）} {mathrm {d} x}} = varphi（x）+{frac {v（x）} {g {a}}（x）}}}}}$

と

第三党の順序の理論 [ 編集 | ソーステキストを編集します ]

第三党の理論の理論でも 大きな変形 キャッチ、理論IIの単純化。順序はここにも適用されなくなりました。

第3パーティの順序のくちばし理論が必要なアプリケーションケースはzです。 B.大きな水深の船舶からのオフショアパイプラインの敷設。ここでは、レベルの静的ケースとしてのみ。

非常に長いパイプストランドが車両から海底に垂れ下がっており、ロープのように湾曲していますが、硬いです。非線形微分方程式はこちらです。

{displaystyle ei、varphi ”（s）-h、sin varphi（s）+（ws -v）cos varphi（s）= 0}

と

座標 ${displaystyleS}$
傾斜の角度 ${displaystyle varphi}$

{displaystyle sin varphi（s）= {frac {partial z（s）} {partial s}}}}}

{displaystyle cos varphi（s）= {frac {partial x（s）} {partial s}}}}}

${displaystyle h}$
長さあたりの重量 ${displaystyle in}$
計算サイズ ${displaystyle v}$

レオナルド・ダ・ヴィンチによる主に精神的な実験の後、ガリレオ・ガリレイのバルケン理論が正当化されました。クロード・ルイス・マリー・アンリ・ナビエの仕事で、予備的な古典的なバー理論が達成されました。

レオナルド・ダ・ヴィンチの古典的な曲げ理論の「父親」からナビエへ：

レオナルド・ダ・ヴィンチ（1452–1519） – ワイヤーの列車の試み
ガリレオガリレイ（1564–1642） – メカニックと地元の動きを演じる2つの新しい科学に関する数学的なスピーチとデモンストレーション ：大理石の柱、ロープ、ワイヤの列車強度（初日）、梁の破壊強度に関する考慮事項（2日目）
Edme Mariotte（1620–1684） – 繊維の線形分布クロスセクション上に伸びる、二重 – 相互ビーム交差セクションの半分の中性繊維
ロバート・ホーク（1635–1703） – ストレッチングと張力の間の比例（Hookesches Law）
Isaac Newton（1643–1727） – 力のバランス、無限のIME計算
Gottfried Wilhelm Leibniz（1646–1716） – 無限の計算、抵抗モーメント ^[12番目]
Jakob I Bernoulli（1655–1705） – 理論を簡素化する仮定：レベルと垂直の交差領域のビーム軸の垂直軸は、曲げ後、ビーム軸にも垂直です
Leonhard Euler（1707–1783） – 静的に決定されていないシステム（四本脚テーブル）を最初に治療しようとする試み、ロッドのねじれの検査（2次の理論）
Charles Augustin de Coulomb（1736–1806） – 無限の計算に関連するビーム、アーチ型、地球圧力理論の最初の表現。構築統計は「科学的主題」になります
ヨハンアルバートエイテルワイン（1764–1848） – ソリューション静的に不定システム：スループットキャリア
クロード・ルイス・マリー・アンリ・ナビエ（1785–1836） – 彼の作品は「統計の構築の憲法上の段階」を表しています。彼は彼の中でリードします 技術的な曲げ理論 弾性ライン（Bernoulli、Euler）の数学的機械分析と主にエンジニアリングベースのビーム統計。
Georg Rebhann（1824–1892） – 単純な対称交差セクションの曲げ張力検出のための1856年の式に示されています。

D.グロス、W。ハガー、J。シュリンクス、W。A。ウォール： 技術力学。 バンド1–3、スプリンガー、ベルリン2006 /2007、 DNB 550703683 。
IstvánSzabó： 技術力学の紹介。 Springer、Berlin 2001、ISBN 3-540-67653-8。
ピーター・グムマート、カール・カール・レコルリング： 力学。 Vieweg、Braunschweig 1994、ISBN 3-528-28904-X。
Karl-Eugen Kurrer： 建設統計の歴史。バランスを探しています 、Ernst Und Son、Berlin 2016、pp。88f。、pp。395–412およびpp。452–455、ISBN 978-3-433-03134-6。

↑ FritzStüssi： 私を罰するために 第4版。 1971年、ISBN 3-7643-0374-3、173ページから
↑ ピヒラー、ベルンハルト。 Eberhardsteiner、Josef： Baustatik vo – lva-no。202.065 。 WHO 2016、ISBN 978-3-903024-17-5、 2.7.1 Queuranteile と 10.2クロス共有の選択されたロードメンバー （ TU出版社 [2016年12月10日にアクセス]）。 TU出版社（記念のオリジナル 2016年3月13日から インターネットアーカイブ ）） 情報： アーカイブリンクは自動的に使用されており、まだチェックされていません。指示に従ってオリジナルとアーカイブのリンクを確認してから、このメモを削除してください。 @初め @2
↑ オリバー・ロムバーグ、ニコラウス・ヒンリッヒ：メカニックの前にパニックに陥らないでください！ – エンジニアリングコースの古典的な「ゆるい」でのキャスセスと楽しみ。の：パニックなしで勉強します。 8番目、改訂版。バンド 4 。 Vieweg+Teubner Verlag、2011、ISBN 978-3-8348-1489-0（349ページ、 springer.com [PDF]初版：1999）。
↑ B. Kauschinger、St。Ihlenfeldt： 6.運動学。 （もはやオンラインで利用できなくなりました）からアーカイブされていますオリジナル午前 2016年12月27日 ; 2016年12月27日にアクセス。
↑ JürgenFröschl、Florian Achatz、SteffenRödling、Matthias Decker：クランクシャフトの革新的なコンポーネントテスト概念。の： MTZエンジンマガジン。バンド 71 、いいえ。 9 。 Springer、2010、 S. 614–619 （ springer.com ）。
↑ ^a^b ハーバートマング、Gホフステッター： 強度理論。 ed。：Springer Verlag。（3.エディション）。ウィーン /ニューヨーク2008、ISBN 978-3-211-72453-8、6.4 “通常の電圧”、 S. 156 （487 S.、 springer.com ）。
↑ メインの記事：Biegelinieを参照してください
↑ バー全体に重い関数と統合することが可能です
↑ 豆線の対称性により、ねじれ線の抗測量が続きます ${displaystyle textStyle w ‘（x = {frac {l} {2} {2}}^{ – }）= -w’（x = {frac {l} {2}}^{+}}}$
↑ ^a^b^c^d Bernhard Pichler： 202.068 Construction Statics 2 。 WS2013エディション。ウィーン2013、 VO_06_THIIO_UENVERGUNGS- （ウィーン工科大学のオンラインプラットフォーム）。
↑ ^a^b^c ピヒラー、ベルンハルト。 Eberhardsteiner、Josef： Baustatik vo lva-no。202.065 。 ed。：Tu Verlag。 SS2016エディション。 Tu Verlag、Vienna 2016、ISBN 978-3-903024-17-5、 レベルの線形安定理論 （520ページ、ウィーン工科大学のグラフィックセンター [2017年1月12日にアクセス]）。ウィーン工科大学のグラフィックセンター（記念のオリジナル 2016年3月13日から インターネットアーカイブ ）） 情報： アーカイブリンクは自動的に使用されており、まだチェックされていません。指示に従ってオリジナルとアーカイブのリンクを確認してから、このメモを削除してください。 @初め @2
↑ IFBS： 8.3ガリレオの曲げ理論から砂のレベル理論へ ご参照ください： 大きな数学者が介入します （記念 2016年3月15日から インターネットアーカイブ ））