
3つの個々の個別が体の軸z、x ‘、z “の回転の結果として体を回す。
独自の座標系: 腐敗
修正された参照システム: 青
Eulerschen Winkel (また オイラーショップ )、スイスの数学者であるレオンハルト・オイラーにちなんで名付けられたのは、3次元ユークリッド領域の固体体の方向(回転)を記述するために使用できる3つの角度の文です。 [初め] あなたは通常一緒にいます
 または
または
 専用。たとえば、身体は(理論物理学で)ロータリーまたは車両、船、または飛行機である場合があります。天文学では、「身体」は天体の鉄道の鉄道でもあります。
専用。たとえば、身体は(理論物理学で)ロータリーまたは車両、船、または飛行機である場合があります。天文学では、「身体」は天体の鉄道の鉄道でもあります。
オイラーの角度は、本体の回転の代わりに、別のデカルト座標系に関するデカルト座標系の位置を記述することもでき、したがって、座標変換に使用されます。ねじれた座標系は、多くの場合、回転したボディに「取り付けられています」。その後、1つは話します 身体 座標系と元の座標系に名前を付けます スペース – プルーフ 。
回転は、体を3つのeulerwinkelの周りの元の位置から、座標軸の周りに変えることによって生成されます。軸を選択するためのさまざまな規則があります。
- 実際のeulerwinkel: 1番目と3番目の回転は、同じ座標軸(例:Z軸、X軸、Z軸の周りの回転)の周りで行われます。
- KardanWinkel また Tait-Bryanストア :3つの回転はすべて、異なる座標軸を中心に回転します(例:x軸、y軸、z軸など)。
2番目と3番目の回転のいずれかが、以前に回転した座標軸を回転します( 本質的 ローテーション)
または常に元の座標軸の周り( 外因性 回転)。
3つの個別ターンで構成される回転は、マトリックスで説明できます。これは、3つの基本回転行列の積としてそれに応じて表すことができます。アプリケーションに応じて、さまざまなマトリックスを確認します。
- 回転した(ボディフェスティバル)からオリジナル(耐性)座標系への座標変換の変換マトリックス、
- 宇宙から耐性への座標変換のための変換マトリックス – 防御座標系、
- 耐性座標系に関する回転の撮影。
ロットは、最新の1600年以来、3つの角度で記述されています。そのため、ヨハネス・ケプラーは 新しい天文学 3つの角度で黄道に関連するマルスバーンの向き。ポイントの回転を計算できる代数的記述は、1775年から深さを増やすためにLeonhard Eulerによってのみ策定されました。 [2] 最初の作品で [3] 画像マトリックスの要素に対応する9つの係数は、動きの長さの長さのために互いに独立していないが、3つの独立した角度のみで定義されていることを示しました。ただし、これらはここで扱われるフクロウの角度ではなく、幾何学的な意味のない純粋な算術サイズです。この作業は、追加で今日名前が付けられた回転定理を証明したことが証明されたため、固定点を持つすべての実際の動きが軸の周りの回転であることが証明されたため、特によく知られています。彼は、この結果から生じる評価を発見しました。この結果は、回転の方向性コサインと回転角の方向性コサインによってパラメーター化され、次の2番目の作業でパラメーター化されました。 [4]

店

、

、

仕事から
[5] オイラーによって
3分の1で、郵便局所のみが公開されています [5] 彼はついに3つの角度を率いました
 、
、
 と
と
 彼がボディフェスティバルの宇宙耐性座標への変革を説明し、それが今日彼にちなんで名付けられた角度に一致するものを説明したものです。彼の手順は、今日の現在の手順とは大きく異なり、1つの座標系が3つの連続した座標軸の周りで他の座標系に転送されます。
彼がボディフェスティバルの宇宙耐性座標への変革を説明し、それが今日彼にちなんで名付けられた角度に一致するものを説明したものです。彼の手順は、今日の現在の手順とは大きく異なり、1つの座標系が3つの連続した座標軸の周りで他の座標系に転送されます。
最初の作品に似たオイラーの議論ですが、より安価なアプローチになります [5] :s。 50 3つの角度で
 、
、
 と
と
 なぜなら、ここ – 現代の話す方法で – 彼は線の正規性だけでなく、変換マトリックスの列の列のそれも使用していたからです。彼らの幾何学的な意味を明確にするために、彼は交差点を見ました
なぜなら、ここ – 現代の話す方法で – 彼は線の正規性だけでなく、変換マトリックスの列の列のそれも使用していたからです。彼らの幾何学的な意味を明確にするために、彼は交差点を見ました
 、
、
 、
、
 ユニットボールと対応する交差点を備えた空間耐性座標系の
ユニットボールと対応する交差点を備えた空間耐性座標系の
 、
、
 、
、
 体の長さのシステムとアーチのコシヌスが
体の長さのシステムとアーチのコシヌスが
 、
、
 、…、
、…、
 変換方程式の係数は正確です。だからそうです
変換方程式の係数は正確です。だからそうです
 間の角度
間の角度
 – そしてその
– そしてその
 -軸。さらに、球状の三角法を使用することが示されています
-軸。さらに、球状の三角法を使用することが示されています
 角度
角度
 ボールトライアングルで
ボールトライアングルで
 と
と
 角度
角度
 ボールトライアングルで
ボールトライアングルで
 は。今日、対応する角度はそうではありません
は。今日、対応する角度はそうではありません
 – レベルですが、結び目からそれまで
– レベルですが、結び目からそれまで
 測定; X-Y-Xのシーケンスに今日使用されているフクロウの角度との接続は、
測定; X-Y-Xのシーケンスに今日使用されているフクロウの角度との接続は、
 、
、
 と
と
 。
。
ラグランジュは1788年に持ち込まれました 分析力学 [6] 変換方程式の2つの派生。最初 [6] :s。 381–388 角度の名前を除いて正しい(彼らはそれを呼ばれている
 、
、
 と
と
 )本質的にオイラーのもの。二番目 [6] :s。 398–401 Z-X-Zシーケンス-Againの最新の詳細な表現と他の角度名と一致します(
)本質的にオイラーのもの。二番目 [6] :s。 398–401 Z-X-Zシーケンス-Againの最新の詳細な表現と他の角度名と一致します(
 、
、
 、
、
 )。
)。

座標変換、標準X条約のシーケンスのシーケンス
青 :開始点の座標系
緑 :XYレベルのまっすぐ、X軸の中間層をまっすぐに切る
腐敗 :ターゲットの座標系
以下では、グラフィックに隣接するように、小さな文字が付いた開始点(グラフィックブルー)の座標系の軸は
 、
、
 と
と
 、対応する大文字を持つターゲット(グラフィックレッド)の軸
、対応する大文字を持つターゲット(グラフィックレッド)の軸
 、
、
 と
と
 専用。
専用。
幾何学的説明 [ 編集 | ソーステキストを編集します ]
 –
–
 レベルと
レベルと
 –
–
 – 直線でベインカット
– 直線でベインカット
 (ノットライン)。これは垂直にあります
(ノットライン)。これは垂直にあります
 -axse and on
-axse and on
 -軸。
-軸。
ここで説明するオイラー角のバージョン。
 の
の
 – ノットラインと角度に到達します
– ノットラインと角度に到達します
 ノードラインから
ノードラインから
 -een軸はそれと呼ばれます 標準-Xコンベンション 。したがって、 標準-Yコンベンション の角度
-een軸はそれと呼ばれます 標準-Xコンベンション 。したがって、 標準-Yコンベンション の角度
 – ノットラインからノードラインからの軸
– ノットラインからノードラインからの軸
 -een測定。
-een測定。
標準X規則は通常、古典物理学で使用されます。ここの代わりに
 、
、
 と
と
 通常、角度はあります
通常、角度はあります
 、
、
 と
と
 専用。一方、量子力学では、標準I条約が優先されています。特に、SO3ロータリーグループの表現は、いわゆるウィグナーDマトリックによってそれに応じてパラメーター化されています。
専用。一方、量子力学では、標準I条約が優先されています。特に、SO3ロータリーグループの表現は、いわゆるウィグナーDマトリックによってそれに応じてパラメーター化されています。
本質的な回転による説明 [ 編集 | ソーステキストを編集します ]
回転
 、それはそれです
、それはそれです
 – その中のシステム
– その中のシステム
 – システムターンは、3つの回転に分割できます。標準Xコンベンションでは、これは次のとおりです。
– システムターンは、3つの回転に分割できます。標準Xコンベンションでは、これは次のとおりです。
このターンでは、新しい座標系が連続して作成されます。
回転
 周りの回転も同様です
周りの回転も同様です
 – 到達、周りの回転
– 到達、周りの回転
 – 周りの回転を獲得します
– 周りの回転を獲得します
 -軸。全体的なターン
-軸。全体的なターン
 したがって、ターンから出ます
したがって、ターンから出ます
 、
、
 と
と
 一緒:
一緒:
-

したがって、回転軸の順序は次のとおりです。
 -ACHS→
-ACHS→
 -ACHS→
-ACHS→
 – 軸または短い
– 軸または短い
 –
–
 –
–
 。
。
回転のこのような分解は、それぞれが座標軸の周りで回転していることが呼ばれます。 本質的 セットニングシーケンス。
外因性回転による説明 [ 編集 | ソーステキストを編集します ]
同じ回転
 また、元の座標軸を3つの個別のターンを記述することもできます。角度は同じままですが、ターンの順序は回転し、中間層
また、元の座標軸を3つの個別のターンを記述することもできます。角度は同じままですが、ターンの順序は回転し、中間層
 と
と
 固有の回転とは異なります:
固有の回転とは異なります:
最初に体は角度の周りになります
 に
に
 -een軸、その後
-een軸、その後
 に
に
 -axse(間の角度
-axse(間の角度
 – と
– と
 -eenは間でそれと同じです
-eenは間でそれと同じです
 – そしてその
– そしてその
 -axse、すなわち
-axse、すなわち
 )そして最後に角度の周り
)そして最後に角度の周り
 に
に
 -axse(それはそうなるでしょう
-axse(それはそうなるでしょう
 – 結び目の軸
– 結び目の軸
 回転し、その間の角度
回転し、その間の角度
 そしてその
そしてその
 -ACHSです
-ACHSです
 )。
)。
代数的正当化は、一般的なケースのマトリックスヘリパルセクションの下にあります。だからそうです
-
 。
。
元の座標軸が常に回転するようなシーケンスは呼ばれます 外因性 セットニングシーケンス。
したがって、内因性および外因性回転の説明は同等です。ただし、本質的な回転の説明はより記述的ですが、説明は外因性回転によって数学的にアクセスしやすいです。
マトリックスによる説明 [ 編集 | ソーステキストを編集します ]
オイラー角の周りの回転は、回転マトリックスの助けを借りて説明できます。そのエントリは、オイラーウィンケルの副鼻腔とコサイン値です。イメージングマトリックスと座標変換マトリックスを区別します。標準X規則のこれらのマトリックスを以下に示します。
標準I規則のマトリックスは、X軸の周りの回転のための基本回転マトリックスの代わりに、y軸の周りの回転の回転マトリックスを使用することにより、同様に得られます。
フィギュアマトリックス(アクティブ回転) [ 編集 | ソーステキストを編集します ]
で アクティブ回転 ( アリバイ )部屋のポイントとベクトルを回します。座標系が記録されます。回転マトリックス
 この図の画像マトリックスです。回転したベクトルの座標
この図の画像マトリックスです。回転したベクトルの座標
 元のポイントの座標の結果
元のポイントの座標の結果
 ロータリーマトリックスとの乗算により:
ロータリーマトリックスとの乗算により:
-

座標軸(基本回転マトリックス)の周りの回転のイメージングマトリックスは次のとおりです。
-

角度の周りの回転用
 に
に
 – それを獲得します
– それを獲得します
 -ACHS AND THE
-ACHS AND THE
 -軸。
-軸。
複合回転の回転マトリックスは、個々の回転の行列からのマトリックス増殖から得られます。基本回転マトリックスは元の座標軸の周りの回転を記述しているため、外因性シーケンスが使用されます
-

イラストマトリックスを受け取ります
-

TransformationSmatrix [ 編集 | ソーステキストを編集します ]
変換マトリックスは、元の(スペース – プルーフ)座標系からターン(ボディフェスティバル)またはその逆への座標変換を記述します。体耐性座標系からルームフェスティバルへの座標変換の変換マトリックスは、上記のフォーメーションマトリックスと一致します。逆変換のマトリックスは、このマトリックスの転置です。ベクトルがあります
 空間耐性座標系の座標
空間耐性座標系の座標
 そして、ボディフェスティバルの座標
そして、ボディフェスティバルの座標
 適用されます
適用されます
-

と
-

大会 [ 編集 | ソーステキストを編集します ]
実際のeulerwinkelの軸を選択するには、6つの異なる方法があります。誰にとっても、最初と3番目の軸は同じです。 6つのオプションは次のとおりです。
両方 カルダンの角度 (Gerolamo cardanoによると)または テイト・ブライアンの角度 (ピーター・ガスリー・テイトとジョージ・ハートリー・ブライアンにちなんで名付けられました)3つの回転は、3つの異なる軸の周りに行われます。実際のフクロウの角度と同様に、6つの可能なねじれがあります。
ロール、ニック、貪欲な角度:z-ys-x″コンベンション [ 編集 | ソーステキストを編集します ]
説明 [ 編集 | ソーステキストを編集します ]

Z、Y ‘、X’ ‘(Greed-nickロール)のセットニング
青 :raumfestes座標系
緑 :y’-axis = node line n(y ‘)
腐敗 :ボディ耐性座標系
注釈:

ここではネガティブです。
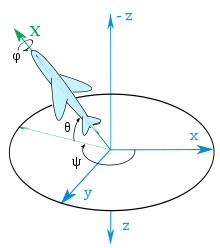
貪欲、ニック、ローラーの角度

航空機の角度として
航空、出荷、自動車建設の使用および標準化(航空:DIN 9300; Automobilbau:DIN ISO 8855)販売シーケンスは、Tait Bryanターンのグループに属しています。基準では、名前は貪欲、ニック、ロールアングル(英語です。 ヨー 、 ピッチ と ロールアングル )3つのオイラーウィンケルに処方されました。 3つの回転により、地球祭は
 – システム(Engl。 ワールドフレーム )ボディフェスティバル
– システム(Engl。 ワールドフレーム )ボディフェスティバル
 -Coodinate系(英語 ボディフレーム )向きを変えた。
-Coodinate系(英語 ボディフレーム )向きを変えた。
本質的な順序
 –
–
 –
–
 (gier-nick roll-anger):
(gier-nick roll-anger):
外因性これは順序に対応します
 –
–
 –
–
 (Roll-nick-Greed角度)。
(Roll-nick-Greed角度)。
小さな文字の代わりに
 、
、
 と
と
 対応する大文字もあります
対応する大文字もあります
 、
、
 と
と
 使用済み。
使用済み。
TransformationSmatrizen [ 編集 | ソーステキストを編集します ]
ボディフェスティバルから空間耐性座標系への座標変換は、マトリックスを介して行われます
-

説明された。宇宙フェスティバルからボディプルーフ座標系への逆変換は、このマトリックスを転置することによって説明されます。 (実際には逆ですが、回転マトリックスの場合、逆は転置されたマトリックスと一致します。)
-

つまり、ベクトルがあります
 空間耐性システムの座標
空間耐性システムの座標
 、
、
 、
、
 そして、身体耐性システムの座標
そして、身体耐性システムの座標
 、
、
 、
、
 適用されます
適用されます
-

と
-

アプリケーションの例 [ 編集 | ソーステキストを編集します ]
重量ベクトル
 地球祭に参加しています
地球祭に参加しています
 -Coodinate系は1つだけです
-Coodinate系は1つだけです
 -komponente(地球の中心に向かって):
-komponente(地球の中心に向かって):
-

航空機への変換は、地球耐性ベクターの乗算によって発生します
 変換マトリックス付き
変換マトリックス付き
 :
:
-

体重は物理的に正しいです
 既存のニックウィンケルで
既存のニックウィンケルで
 たとえば、飛行機でも後方に(負の
たとえば、飛行機でも後方に(負の
 -方向)。
-方向)。
回転軸の順序を選択するために、結果の回転マトリックスは、次の接続(アクティブターン)の助けによって簡単に導出できます。 [7]
グローバル軸の周りの回転マトリックスは既知です。これがすでにねじれた軸の周りに再び回される場合、回転マトリックスは対応するグローバル軸に対応しますが、変換されたベクトルベースに対応します。変換マトリックス(基本変化マトリックス)は、まさに以前の回転です。
なれ
 と
と
 2つのグローバル軸の周りの2つの回転マトリックス
2つのグローバル軸の周りの2つの回転マトリックス
 と
と
 。ロータリーマトリックスを順序に計算します
。ロータリーマトリックスを順序に計算します
 回転マトリックスが2回目の回転のためにあることを観察した場合
回転マトリックスが2回目の回転のためにあることを観察した場合
 基本マトリックス
基本マトリックス
 対応する必要があります。これにより、結果の総射撃行列が得られます
対応する必要があります。これにより、結果の総射撃行列が得られます
 。より多くの回転の場合、証明は同様です。
。より多くの回転の場合、証明は同様です。
3つのアクティブターン(Aが最初に実行され、次にB、次にc)で総射撃行列が結果をもたらします
 の使用中
の使用中
 、
、
 。
。
この表現は、連続した軸の回転シーケンスの回転マトリックスの回転マトリックスは、逆の順序ではあるが、グローバル座標軸の周りの回転マトリックスの単純な乗算に起因することを示しています。
軸を使用した得られた座標系
 、
、
 と
と
 SO -CALLED BODY -PROOFシステムです。角度
SO -CALLED BODY -PROOFシステムです。角度
 と
と
 の場所を与えます
の場所を与えます
 – 耐性システム(「回転」および「傾斜」)と比較したマッケス;角度
– 耐性システム(「回転」および「傾斜」)と比較したマッケス;角度
 あなたの周りの体の道を説明します。これは、次の名前の規則に対応しています。
あなたの周りの体の道を説明します。これは、次の名前の規則に対応しています。
関連するロータリーマトリックスをオイラー角に割り当てるイラストには、この割り当てが局所的に可逆的ではなく、ジンバルロックについて話す重要なポイントがあります。上階の場合。 xまたはyの規則は、2番目の回転角がゼロになり、最初の回転の回転ベクトルが2番目の回転の回転ベクトルと同じである場合に常に発生します。しかし、それはそれが周りの回転のためであることを意味します
 -Ouler-Winkelと同じように
-Ouler-Winkelと同じように
 与えます。
与えます。
航空基準の後に位置角を定義するとき、重要なポイントが含まれています
 。
。
カート・マグナスの後 [8] ジャイロの問題があります
 フクロウの角度(Xコンベンション)を使用しない可能性があり、代わりにCardWortを使用します。
フクロウの角度(Xコンベンション)を使用しない可能性があり、代わりにCardWortを使用します。
Euler-Winkelには、回転を表すためのいくつかの欠点があります。
- 上記の特異点は、異なるオイラーターンによって単一の回転を表すことができることを意味します。これは、ジンバルロックとして知られる現象につながります。
- オイラーシステムでの回転の正しい組み合わせは、回転の軸が変化するため、直感的に指定することはできません。
フクロウの角度ではなく、すべての回転は、その方向を通じて軸の位置と回転感覚を指定するベクトルによって指定することもできます。 [9] または直交テンソル)。オリエンテーションを説明し、これらの欠点を部分的に回避する別の方法は、四項です。

Alpha2ガンマ2相合金におけるガンマティアルのテクスチャ極フィギュア。 [十]
理論物理学では、オイラーの角度を使用して剛体を記述します。実用的なアプリケーションは、よく知られているカルダンサスペンションをもたらします [11] 技術的なメカニズム。
車両の場合、主要な状況のオイラーウィンケルは、ロールニックグリード角と呼ばれます。
結晶学では、単結晶回折計の円を記述するオイラー角度(オイラー角に対応し、EUL-Wiegeと呼ばれる2つの垂直回転回路からのカルダン懸濁液を使用) [12番目] テクスチャの方向密度分布関数を説明するために使用されます。
天文学では、オイラーシェンの角度は他の名前の中にあります bahnement オブジェクトの。
コンピューターグラフィックスでは、オブジェクトの方向を記述するためにオイラーの角度を使用します。
ソリッドステートNMRでは、オイラーの角度が理論的記述とスペクトルのシミュレーションに使用されます。
- ↑ ハーバートゴールドスタイン、チャールズP.プールジュニア、ジョンL.サフコ: クラシックメカニック 。 3番目、完全および拡張版。 Wiley-VCH、2006、ISBN 3-527-40589-5、 S. 161 ff 。 ( 限られたプレビュー Google Book検索で)。 「3つの連続したターンを使用して、デカルト座標系から別の系への変換を実行できます。これは、特定の順序で実行する必要があります。」
- ↑ Hui Cheng、K。C。Gupta: 最終回転に関する歴史的なメモ 。の: Journal of Applied Mechanics 。 バンド 56 、 いいえ。 初め 、1989年3月、 S. 139–145 、doi: 10.1115/1,3176034 ( 全文 [PDF; 2018年12月13日にアクセス])。
- ↑ L. eulerus: すべての剛体の翻訳のための一般的な式 。の: 新しい解説科学アカデミーペトロポリタナエ 。 バンド 20(1775) 、1776、 S. 189–207 ( オンライン 英語翻訳[PDF; 188 KB ; 2018年12月13日にアクセス] 移行 ここでの動きはあります)。
- ↑ L. eulerus: 決定する新しい動機の方法 。の: 新しい解説科学アカデミーペトロポリタナエ 。 バンド 20(1775) 、1776、 S. 208–238 ( オンライン [PDF; 1.6 MB ; 2018年12月13日に取得]方程式は§13にあります)。
- ↑ a b c Leonardus eulerus: 固定された携帯電話の周りの体の動き 。の: レナードオイラーオペラPOTEMA数学と物理学:1844年に開示 。 バンド 2 、1862年、 S. 43–62 ( オンライン [PDF; 1.4 MB ; 2018年12月13日にアクセス])。 – 関連するイラスト
- ↑ a b c 納屋: 分析力学 。 Göttingen1797( スキャン [PDF; 2018年12月13日にアクセス]オリジナルタイトル: 分析力学 。 1788年。フリードリッヒ・ウィルヘルム・アウグスト・マーハルトによる翻訳)。
- ↑ 詳細な証拠は、G。Fischer: 線形代数学習帳と分析ジオメトリ。 2012年第2版、5.3.6
- ↑ マグナス、クライゼル、スプリンガー、1971年、p。32
- ↑ ハーバートゴールドスタイン、チャールズP.プール、ジュニア、ジョンL.サフコ、シニア: クラシックメカニック 。 3.エディション。 John Wiley&Sons、2012、ISBN 978-3-527-40589-3。
- ↑ Liss KD、Bartels A、Schreyer A、Clemens H: 高エネルギーX線:材料科学と物理学の高度なバルク調査のためのツール 。の: テクスチャ微細構造。 35年、 いいえ。 3/4 、2003年、 S. 219–52 、doi: 10.1080/07303300310001634952 。
- ↑ とりわけ、ユーラーの角度とカルダニアンサスペンションとの関係はあります。次の本の第11.7章で発表しました:U。Krey、A。Owen: 基本的な理論物理学 – 簡潔な概要。 Springer-Verlag、ベルリン2007。
- ↑ Euler-Wiege、Geosciencesの辞書、Spectrum








 または
または  専用。たとえば、身体は(理論物理学で)ロータリーまたは車両、船、または飛行機である場合があります。天文学では、「身体」は天体の鉄道の鉄道でもあります。
専用。たとえば、身体は(理論物理学で)ロータリーまたは車両、船、または飛行機である場合があります。天文学では、「身体」は天体の鉄道の鉄道でもあります。 


 、
、  、
、  ユニットボールと対応する交差点を備えた空間耐性座標系の
ユニットボールと対応する交差点を備えた空間耐性座標系の  、
、  、
、  体の長さのシステムとアーチのコシヌスが
体の長さのシステムとアーチのコシヌスが  、
、  、…、
、…、  変換方程式の係数は正確です。だからそうです
変換方程式の係数は正確です。だからそうです  間の角度
間の角度  – そしてその
– そしてその  -軸。さらに、球状の三角法を使用することが示されています
-軸。さらに、球状の三角法を使用することが示されています  と
と  は。今日、対応する角度はそうではありません
は。今日、対応する角度はそうではありません  – レベルですが、結び目からそれまで
– レベルですが、結び目からそれまで  測定; X-Y-Xのシーケンスに今日使用されているフクロウの角度との接続は、
測定; X-Y-Xのシーケンスに今日使用されているフクロウの角度との接続は、  、
、  と
と  。
。  、
、  と
と  )本質的にオイラーのもの。二番目 [6] :s。 398–401 Z-X-Zシーケンス-Againの最新の詳細な表現と他の角度名と一致します(
)本質的にオイラーのもの。二番目 [6] :s。 398–401 Z-X-Zシーケンス-Againの最新の詳細な表現と他の角度名と一致します(  、
、  、
、  )。
)。  と
と  、対応する大文字を持つターゲット(グラフィックレッド)の軸
、対応する大文字を持つターゲット(グラフィックレッド)の軸  と
と  専用。
専用。  の
の  ノードラインから
ノードラインから  と
と  、
、  と
と  専用。一方、量子力学では、標準I条約が優先されています。特に、SO3ロータリーグループの表現は、いわゆるウィグナーDマトリックによってそれに応じてパラメーター化されています。
専用。一方、量子力学では、標準I条約が優先されています。特に、SO3ロータリーグループの表現は、いわゆるウィグナーDマトリックによってそれに応じてパラメーター化されています。  – その中のシステム
– その中のシステム  – システムターンは、3つの回転に分割できます。標準Xコンベンションでは、これは次のとおりです。
– システムターンは、3つの回転に分割できます。標準Xコンベンションでは、これは次のとおりです。  – 到達、周りの回転
– 到達、周りの回転  -軸。全体的なターン
-軸。全体的なターン  、
、  と
と  一緒:
一緒: 
 と
と  固有の回転とは異なります:
固有の回転とは異なります: -eenは間でそれと同じです
-eenは間でそれと同じです 
 この図の画像マトリックスです。回転したベクトルの座標
この図の画像マトリックスです。回転したベクトルの座標  元のポイントの座標の結果
元のポイントの座標の結果  ロータリーマトリックスとの乗算により:
ロータリーマトリックスとの乗算により: 


 そして、ボディフェスティバルの座標
そして、ボディフェスティバルの座標  適用されます
適用されます 


 –
–  、
、  と
と  使用済み。
使用済み。 

 、
、  、
、  そして、身体耐性システムの座標
そして、身体耐性システムの座標  、
、  、
、  適用されます
適用されます 

 地球祭に参加しています
地球祭に参加しています 
 変換マトリックス付き
変換マトリックス付き  :
: 
 と
と  。ロータリーマトリックスを順序に計算します
。ロータリーマトリックスを順序に計算します  回転マトリックスが2回目の回転のためにあることを観察した場合
回転マトリックスが2回目の回転のためにあることを観察した場合  対応する必要があります。これにより、結果の総射撃行列が得られます
対応する必要があります。これにより、結果の総射撃行列が得られます  。より多くの回転の場合、証明は同様です。
。より多くの回転の場合、証明は同様です。  の使用中
の使用中  、
、  。
。  、
、  と
と  SO -CALLED BODY -PROOFシステムです。角度
SO -CALLED BODY -PROOFシステムです。角度  と
と  与えます。
与えます。  。
。  フクロウの角度(Xコンベンション)を使用しない可能性があり、代わりにCardWortを使用します。
フクロウの角度(Xコンベンション)を使用しない可能性があり、代わりにCardWortを使用します。
Recent Comments