一 最小限のエリア 部屋のエリアが最小限のエリアです。たとえば、このような形状は、対応するフレーム(風のリングなど)を介して張力をかけられている場合、石鹸皮を引き受けます。
数学的言語では、最小限の領域が領域のコンテンツ機能の重要なポイントです
-
 。
。
これがサイズです
 と
と
 ために
ために
 説明(Hesse-Matrixを参照)。最小限の面積には必ずしも最小限の面積があるわけではなく、面積コンテンツ関数の静止ポイントにすぎないことに注意してください。 2つの部屋の寸法におけるエリアコンテンツ関数の最初の変動の消失は、考慮されたマニホールドが十分に規則的である場合、中央の曲率hを消滅させるのと同等であることを示すことができます。
説明(Hesse-Matrixを参照)。最小限の面積には必ずしも最小限の面積があるわけではなく、面積コンテンツ関数の静止ポイントにすぎないことに注意してください。 2つの部屋の寸法におけるエリアコンテンツ関数の最初の変動の消失は、考慮されたマニホールドが十分に規則的である場合、中央の曲率hを消滅させるのと同等であることを示すことができます。
19世紀以来、最小限の分野は数学的研究に焦点を当てています。ベルギーの物理学者ジョセフ・プラトーによる実験は、これに大きな貢献でした。

最小限の領域の例としてのenneperエリア
2つの変数の存在理論に関する例外 [ 編集 | ソーステキストを編集します ]
2次元パラメーター領域は常に特別な機能です。機能理論のツールを使用すると、より高い部屋の寸法よりもはるかに多くの声明を達成できるためです。その結果、たとえば、Riemannイメージのあるパラメーター領域として、いつでも地区ディスクに引き出すことができます。均一化率は、2つの部屋の寸法にも適用されます。パラメトリックトラップを解くときに必要な等温パラメーターを導入できます。そのため、この理論は2つの変化しやすいことで特に広く開発されています。
バリエーションの問題としての定式化 [ 編集 | ソーステキストを編集します ]
エリアは、すべてのポイントで中央の曲率ゼロがある場合、まったく最小限のエリアです。これは、最小限の領域が中程度の曲率によって規定されている領域の特殊なケースであることを意味します。これらは変動計算からも逃げることはありません。
-
 。
。
この関数の必要な最小条件としてのオイラー方程式は、Franz Rellichに従って名前が付けられたH表面システムです
-
 。
。
ここは
 中央の曲率。
中央の曲率。
パラメトリックケース [ 編集 | ソーステキストを編集します ]
この機能のために、局所的な最小値の存在の問題は、有限長の所定の安定した周辺曲線で生じます。このタスクは、文献でも説明されています プラットフォームの問題。 中程度の曲率に対する小ささの条件を仮定すると、最小面積が発生した場合に常に満たされているため、この質問は積極的に答えることができます。自分を納得させるために、あなたは同時に最小化します
 エネルギー機能
エネルギー機能
-

いわゆる高速パラメーターの導入中。
1884年、ヘルマン・アマンダス・シュワルツは刑を見せた
- 性別ゼロ(つまり、穴のない)から、着実に区別され、閉じた、閉じた方向のある表面の量の量では、ボールは表面であり、与えられた表面の最大の空間を変化させます。
分岐点 [ 編集 | ソーステキストを編集します ]
どのソリューションを置きます
 満たされた、呼ばれます ブランチポイント。 これらのポイントでパラメーター化が特異になる可能性があるため、分岐点は興味深いものです。ソリューションがもはや領域ではない可能性はさらに悪化しますが、曲線のみです。
満たされた、呼ばれます ブランチポイント。 これらのポイントでパラメーター化が特異になる可能性があるため、分岐点は興味深いものです。ソリューションがもはや領域ではない可能性はさらに悪化しますが、曲線のみです。
現在、CarlemanとVekuaによる作品に大きく触発された機能的な考慮事項は、ソリューションが最終的に多くのそのような分岐を持つことができることを提供しています。残念ながら、上記の方法では、そのような分岐点は先験的に除外されていません。それはガリバー・アルト・オッサーマンの精巧な刑とのみです。したがって、枝のないH表面のクラスでプラットフォームの問題を解決したいという願望があります。これはまだ未解決の質問です。
非パラメトリックケース、最小面積方程式 [ 編集 | ソーステキストを編集します ]
ただし、上記の方法は定数にのみつながります
 成功へ。平均曲率もソリューションに依存している場合でも、グラフが発生した場合でも何かをすることができます。
成功へ。平均曲率もソリューションに依存している場合でも、グラフが発生した場合でも何かをすることができます。
 グラフ、彼はaとして書きます
グラフ、彼はaとして書きます
 と関数
と関数
 満たされた 処方された中程度の曲率の非パラメトリック方程式
満たされた 処方された中程度の曲率の非パラメトリック方程式
-
 。
。
領域が最小の場合、h = 0と方程式は最小面積方程式と呼ばれます。 [初め]
深い生計の結果は、この部分的な微分方程式のディリクレの問題の溶解度を提供し、小ささ条件やその他の技術的要件を仮定します。一意性は、2つのソリューション間の違いの最大原理によっても明らかにされています。のためにグラフもあります
-

常にブランチフリー。
ここでは、さまざまな最小領域のいくつかの例が、3次元ユークリッド空間に示されています。それらのいくつかは、自己カットなしで3次元空間に埋め込むことはできません。最初の例が示すように、他の人は定義領域の端まで継続的に継続することはできません。
H. F. Scherkの最小面積 [ 編集 | ソーステキストを編集します ]

パラメーターC = 1へのScherkの最小領域の接続コンポーネント
ハインリッヒフェルディナンドシェルクの最小面積(1835):非パラメトリック最小領域方程式のすべてのソリューションを探しています
 書いたことと条件
書いたことと条件
 、
、
 十分です。最初にこの構造を最小領域方程式に挿入し、保存します。
十分です。最初にこの構造を最小領域方程式に挿入し、保存します。
-

-

同等の変更を提供します
-

とともに
 。通常の微分方程式の理論によれば、初期値の問題には正確に1つの解があります
。通常の微分方程式の理論によれば、初期値の問題には正確に1つの解があります
-
 データに
データに

と
-
 データに
データに

これらのソリューションはそうです
-

と
-


パラメーターC = 0.2のScherkschen最小領域のいくつかのコンテキストコンポーネント
ここで私たちはまだ最初の値にあることに注意していません
 と
と
 とともに
とともに
 異なる可能性があります。ただし、構造的条件と機能自体が通常の微分方程式では発生しないという事実のため、発生する可能性があります
異なる可能性があります。ただし、構造的条件と機能自体が通常の微分方程式では発生しないという事実のため、発生する可能性があります
 要求。だから私たちは受け取ります:
要求。だから私たちは受け取ります:
-

正方形のこの最小領域に気づきます
-

説明し、継続できません。この領域は、3次元空間にグラフとして寝かせます。
ダス・カテノイド [ 編集 | ソーステキストを編集します ]

カテノイドからパラメーターC = 1
チェーンラインをX軸の周りに回転させると、3次元のスペースAカテノイドに埋め込まれた最小面積も取得します。カテノイドは、回転領域でもある唯一の最小領域です。方程式の肯定的なパラメーターc> 0を満たしています
-

これは、実験的に発見された血小板の最初の解決策の1つでした。エッジデータは2つの円形リングで、コーンまたはシリンダーの上限と下のエッジ曲線を形成しました。
最小限の領域としてのカテノイドは、1740年頃のレオンハルトオイラーから来ています。
らせんエリア [ 編集 | ソーステキストを編集します ]
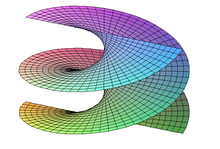
parameter c = 1からhelikoid
スパイラルエリアまたはヘリコイドは、カテノイドと密接に関連しています。この領域は、不安定であるが等尺性の変形のためにカテノイドから出現します。パラメーターc> 0に、次の方程式を満たしています。
-

-

-

この最小面積は、3次元空間にも埋め込まれています。
最小限のエリアとしてのスパイラルエリアは、Jean-Baptiste Meusnier de La Place(1776)から来ています。ヘリクスにはトポロジカルな性別があります。デイビッドアレンホフマンと同僚は、1990年代にコンピューター援助で建設されました。これにより、無限でarbitrary意的なトポロジーの性別を備えた最小限の領域、コンピューター補助具は無限の性別と性別のみのためのものでした(Michael Wolf、Hoffman、Matthias Weber 2009)。 0の場合、ヘリシド(特別なケースとしてもカテノイドとしても含まれます)とレベルは、唯一の完全なミント可能な最小領域です(William Meeks、Harold William Rosenberg 2005)。
ヘンネバーグエリア [ 編集 | ソーステキストを編集します ]
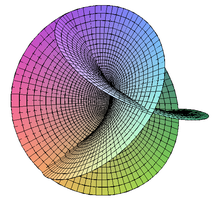
Henneberg Minimalエリア
ヘンネバーグエリアは、3次元ユークリッド空間に浸ることのイメージである最小限の領域の例ですが、3次元ユークリッド空間に埋め込むことはできません。あなたの決定方程式は次のとおりです。 [2]
-

-

-

さらに、この領域を方向づけることはできません:あなたはこの領域のどちらの側面を鮮明に話すことができます その上 そしてどちら 下 は。
彼女は、1875年に彼の論文で彼女を紹介したLife RightによるとHennebergと名付けられました。
部屋の寸法が高い場合、血小板の問題へのアクセスは困難です。ここでは、ソリューションをグラフとして理解する機会しかありません。グラフの最小面積方程式が記述されています
-
 。
。
楕円形の限界価値の問題のソーベンシーが弱いという理論のため、この状況での解決策の存在を保証できます。その後の定期的な考慮事項は、古典的なソリューションを提供します。 2つの部屋の寸法と同様に、2つのソリューション間の違いの最大原理から一意性を取得できます。
最小限の領域に十分な方程式の比較的単純な構造により、Homorphや調和のとれた関数で特に知られているいくつかの既知のステートメントを、2つの変数の最小領域に送信できます。
MaximumPrinzip [ 編集 | ソーステキストを編集します ]
最小限の領域の場合
 不平等が適用されます
不平等が適用されます
-
 。
。
最小面積は、説明されているエリアの端に最大値を帯びます。
イラストの均一化 [ 編集 | ソーステキストを編集します ]
Geodesyでは、そのような等温パラメーターを導入できます。これを行うイラストは呼ばれます イラストの均一化。 最小限の領域のイラストの均一化は、調和のとれた関数です。
レレラン分析チャート [ 編集 | ソーステキストを編集します ]
それらが等温パラメーターにある限り、最小限の領域は、説明されている領域内の実際の分析機能です。これは、パラメータープレゼンテーションを、このポイントの領域の領域の任意のポイントの収束シリーズの増強に発展させることができることを意味します。したがって、それはあなたが好きなように頻繁に区別されます。周辺曲線も1ポイントのポイントにある場合、このポイントの領域の最小面積は、エッジを超えて分析的な方法で継続できます。
バーンスタインとリウヴィルの刑 [ 編集 | ソーステキストを編集します ]
最小限のエリアに関するセルゲイバーンスタインの判決は次のとおりです。
- 全体として
 説明された解決策
説明された解決策
 式を満たすには、非パラメトリック最小面積方程式が必要です
式を満たすには、非パラメトリック最小面積方程式が必要です
-
-

- 一定で
 。
。
高次元への一般化の問題は、アンバーの問題として知られており、エンニオ・デ・ジョルジ、エンリコ・ボンビエリなどによって解決されました。
この文から、最小限の領域のリウビルからの文は次のとおりです。
- 全体として
 限られたソリューションを宣言しました
限られたソリューションを宣言しました
 非パラメトリック最小面積方程式が必要です
非パラメトリック最小面積方程式が必要です
-
-
 。
。
これは、機能理論のリウビル文の類似物です。
最小面積の面積 [ 編集 | ソーステキストを編集します ]
最小面積の面積
 ユニットが正常で
ユニットが正常で
 フォームに書いています
フォームに書いています
-
 。
。
エッジ曲線は単に閉じて着実に区別されると想定する必要があります。
最小限の領域をよりよく理解するためには、彼らが出会う微分方程式のみを見るだけでは十分ではありませんが、決定する必要があります。
複雑な表現 [ 編集 | ソーステキストを編集します ]
等温パラメーターuとvの導入により、最初にH = 0のH表面システムを受け取ります。
-

これにより、フォームの2次方程式が記載されています
-

複雑な変数で
 と
と
 そして、プレゼンテーションを取得します
そして、プレゼンテーションを取得します
-
 と
と
 。
。
複雑な曲線を呼び出します
 条件
条件
 と
と
 十分、1つ 等方性カーブ。 また、エリアを呼び出します
十分、1つ 等方性カーブ。 また、エリアを呼び出します
 それは形で
それは形で
 書いてみましょう スライド面。
書いてみましょう スライド面。
最小領域の一般化された定義は次のとおりです。
- 最小限の領域とは、生成等方性曲線がある滑り面です。
その後、真の最小限の領域が条件を満たします
-
 と
と
 。
。
統合 [ 編集 | ソーステキストを編集します ]
KarlWeierstraßとAlfred Enneperにちなんで名付けられた表現式は、微分形状と機能の理論との関係を提供します。 WeierStrassは現在、機能理論の出現に大きな影響を与えています。この公式は、この比較的新しい数学の枝が真剣に受け止められ、非常に成功した理由の1つでした。彼は、すべての非コンテンツミニマルエリアであることを発見しました
 2つのホロモルフィック関数GおよびHとの積分として。コンポーネントにも同じことが当てはまります。
2つのホロモルフィック関数GおよびHとの積分として。コンポーネントにも同じことが当てはまります。
-
 、
、
-
 、
、
-

このディスプレイフォーミュラにより、最小限の領域の写真が最新のコンピューター代数システムの助けを借りて画像を生成することができます。たとえば、この記事では、メープルプログラムを使用してこれらの式を使用して、最小限の領域の画像が作成されました。
積分 – フリー表現 [ 編集 | ソーステキストを編集します ]
等方方程式h = 0を統合して等方性曲線を決定するだけで十分であることがわかったので、実際の最小領域で受け取ります
 SO -CALLED INTECTLAL -FREE表現
SO -CALLED INTECTLAL -FREE表現
-

-

-

ホロモーフィック機能を備えています
 前提条件
前提条件
 会わなければいけない。このように、レイヤーはこの表現を避けます。今まで、複雑な変数の意味
会わなければいけない。このように、レイヤーはこの表現を避けます。今まで、複雑な変数の意味
 実際の最小領域の長い請求書を明確にする
実際の最小領域の長い請求書を明確にする
-
 また。
また。
 、
、
ここは
 最小領域のユニット通常ベクトル。要約してください: 複雑な数を指定することにより
最小領域のユニット通常ベクトル。要約してください: 複雑な数を指定することにより
 また。
また。
 ユニットは通常のベクトルです
ユニットは通常のベクトルです
 最小エリアを設定します。逆に、ハングします
最小エリアを設定します。逆に、ハングします
 また。
また。
 からのみ
からのみ
 ab。 このセクションの声明は特に本です 基本的な鑑別型 W. BlaschkeとK. Light Whiteが見つけることは、文献も参照してください。
ab。 このセクションの声明は特に本です 基本的な鑑別型 W. BlaschkeとK. Light Whiteが見つけることは、文献も参照してください。
当初、これを機能的に導き出し、積極的に指向したパラメーター変換との不変性を示します。最後に、1つと2次元のケースを明示的に計算します。
派生とパラメーターの不変 [ 編集 | ソーステキストを編集します ]
私たちの最小限の領域は、N次元の実際のベクトル空間におけるM次元の多様性と見なすことができることに注意してください。これは、NASHからの埋め込み率のために常に可能です。最初に説明します メートルテンソル
-

決定要因を使用
-
 。
。
私たちは、M次元の積分としてのm寸法領域のコンテンツが上にあることを覚えています 特性関数 この領域は結果です。特徴的な関数は、群衆のどこでも同じものであり、それ以外の場合は同一のゼロです。これは、表面要素を表現する必要があることを意味します。固定点で接線ベクトルを説明します。
-
 ために
ために

ベクターを選択します
 、システムです
、システムです
-

積極的に配向され、2つの条件です
 と
と
 IとJのすべての賢明な値のために満たされたしたがって、表面要素は次のように書いています。
IとJのすべての賢明な値のために満たされたしたがって、表面要素は次のように書いています。
-

決定要因2の場合
 – マタライズン
– マタライズン
 該当する:
該当する:
-

説明された
 の部分的なマトリックス
の部分的なマトリックス
 それは線からのみです
それは線からのみです
 構成されます。これにより、表面要素をフォームで使用できます
構成されます。これにより、表面要素をフォームで使用できます
-

書く。変換式の助けを借りて、表面要素の同じパラメーター変換、したがって領域の面積の下で不変性を決定します。
1つと2次元コンテンツ [ 編集 | ソーステキストを編集します ]
部屋の寸法では、これは機能的に通常の長さに縮小されます。
-

3次元空間に埋め込まれている2次元領域がある場合、Lagrangeのアイデンティティが得られます。
-

これは機能的な領域に適用されます。
-

- ウィルヘルム・ブラッシュケ、カート・ライト・ホワイト: 基本的な鑑別型 (=数学科学の基本教育。第1巻)。 Springer-verlag、1973年 オンライン。
- ヨハネスC. C.ニッチェ: 最小限の領域に関する講義 (=数学科学の基本的な教育。第199巻)。 Springer-Verlag、1975年。
- デビッド・ギルバーグ、ニール・トルディンジャー: 楕円形の部分微分方程式の二次方程式 (=数学科学の基本教育。第224巻)。 Springer-Verlag、1983年。
- Ulrich Dierkes、Stefan Hildebrandt、AlbrechtKüster、Ortwin Wohlrab: 最小限の表面 (=数学科学の基本教育。295巻と296巻)。 Springer-Verlag、1992年、2巻。
- Stefan Hildebrandt、Anthony Tromba: ボール、サークル、石鹸の泡、幾何学と自然の最適な形状。 Birkhäuser、1996年。
- フリードリッヒ・ソーヴィニー: ジオメトリと物理学の部分微分方程式。 Springer-Verlag、2004 f。、2巻。
- ↑ 最小限の表面 、Mathworld
- ↑ Mathworld、Henneberg最小表面







 と
と  ために
ために  説明(Hesse-Matrixを参照)。最小限の面積には必ずしも最小限の面積があるわけではなく、面積コンテンツ関数の静止ポイントにすぎないことに注意してください。 2つの部屋の寸法におけるエリアコンテンツ関数の最初の変動の消失は、考慮されたマニホールドが十分に規則的である場合、中央の曲率hを消滅させるのと同等であることを示すことができます。
説明(Hesse-Matrixを参照)。最小限の面積には必ずしも最小限の面積があるわけではなく、面積コンテンツ関数の静止ポイントにすぎないことに注意してください。 2つの部屋の寸法におけるエリアコンテンツ関数の最初の変動の消失は、考慮されたマニホールドが十分に規則的である場合、中央の曲率hを消滅させるのと同等であることを示すことができます。 

 中央の曲率。
中央の曲率。  エネルギー機能
エネルギー機能 
 満たされた、呼ばれます ブランチポイント。 これらのポイントでパラメーター化が特異になる可能性があるため、分岐点は興味深いものです。ソリューションがもはや領域ではない可能性はさらに悪化しますが、曲線のみです。
満たされた、呼ばれます ブランチポイント。 これらのポイントでパラメーター化が特異になる可能性があるため、分岐点は興味深いものです。ソリューションがもはや領域ではない可能性はさらに悪化しますが、曲線のみです。  成功へ。平均曲率もソリューションに依存している場合でも、グラフが発生した場合でも何かをすることができます。
成功へ。平均曲率もソリューションに依存している場合でも、グラフが発生した場合でも何かをすることができます。  グラフ、彼はaとして書きます
グラフ、彼はaとして書きます  と関数
と関数  満たされた 処方された中程度の曲率の非パラメトリック方程式
満たされた 処方された中程度の曲率の非パラメトリック方程式 

 書いたことと条件
書いたことと条件  、
、  十分です。最初にこの構造を最小領域方程式に挿入し、保存します。
十分です。最初にこの構造を最小領域方程式に挿入し、保存します。 


 。通常の微分方程式の理論によれば、初期値の問題には正確に1つの解があります
。通常の微分方程式の理論によれば、初期値の問題には正確に1つの解があります 





 と
と  とともに
とともに  異なる可能性があります。ただし、構造的条件と機能自体が通常の微分方程式では発生しないという事実のため、発生する可能性があります
異なる可能性があります。ただし、構造的条件と機能自体が通常の微分方程式では発生しないという事実のため、発生する可能性があります  要求。だから私たちは受け取ります:
要求。だから私たちは受け取ります: 















 フォームに書いています
フォームに書いています 


 と
と  そして、プレゼンテーションを取得します
そして、プレゼンテーションを取得します 

 条件
条件  と
と  十分、1つ 等方性カーブ。 また、エリアを呼び出します
十分、1つ 等方性カーブ。 また、エリアを呼び出します  それは形で
それは形で  書いてみましょう スライド面。
書いてみましょう スライド面。 

 2つのホロモルフィック関数GおよびHとの積分として。コンポーネントにも同じことが当てはまります。
2つのホロモルフィック関数GおよびHとの積分として。コンポーネントにも同じことが当てはまります。 





 前提条件
前提条件  会わなければいけない。このように、レイヤーはこの表現を避けます。今まで、複雑な変数の意味
会わなければいけない。このように、レイヤーはこの表現を避けます。今まで、複雑な変数の意味  実際の最小領域の長い請求書を明確にする
実際の最小領域の長い請求書を明確にする 

 最小領域のユニット通常ベクトル。要約してください: 複雑な数を指定することにより
最小領域のユニット通常ベクトル。要約してください: 複雑な数を指定することにより  ユニットは通常のベクトルです
ユニットは通常のベクトルです 



 、システムです
、システムです 
 と
と  IとJのすべての賢明な値のために満たされたしたがって、表面要素は次のように書いています。
IとJのすべての賢明な値のために満たされたしたがって、表面要素は次のように書いています。 
 – マタライズン
– マタライズン  該当する:
該当する: 
 の部分的なマトリックス
の部分的なマトリックス  構成されます。これにより、表面要素をフォームで使用できます
構成されます。これにより、表面要素をフォームで使用できます 



Recent Comments